When a mass is rotating in a plane about a fixed point, its angular momentum is directed along: a) the radius b) the tangent the orbit c) the line at angle of 45 degree to the plane of rotation d) the axis of rotation
the radius
the tangent the orbit
the line at angle of to the plane of rotation
the axis of rotation
The correct Answer is:d
To solve the question regarding the direction of angular momentum when a mass is rotating in a plane about a fixed point, we can follow these steps:
1. Understanding Angular Momentum:
Angular momentum (→L) of a particle is defined as the cross product of the position vector (→R) and the linear momentum (→p=m→V). Mathematically, it is given by:
→L=→R×→p=→R×(m→V)
2. Identifying the Vectors:
- The position vector →R points from the fixed point (the center of rotation) to the mass.
- The velocity vector →V is tangent to the circular path of the mass.
3. Direction of the Cross Product:
The direction of the angular momentum vector →L is determined by the right-hand rule applied to the cross product →R×→V.
- Point your fingers in the direction of →R (from the center to the mass) and curl them towards →V (the direction of motion).
- Your thumb will then point in the direction of →L.
4. Conclusion on Direction:
Since →R and →V are both in the plane of rotation, the angular momentum →L will be directed perpendicular to this plane. Therefore, the angular momentum is directed along the axis of rotation.
5. Final Answer:
Based on the analysis, the correct option is:
d) the axis of rotation.
Angular momentum (→L) of a particle is defined as the cross product of the position vector (→R) and the linear momentum (→p=m→V). Mathematically, it is given by:
→L=→R×→p=→R×(m→V)
- The position vector →R points from the fixed point (the center of rotation) to the mass.
- The velocity vector →V is tangent to the circular path of the mass.
The direction of the angular momentum vector →L is determined by the right-hand rule applied to the cross product →R×→V.
- Point your fingers in the direction of →R (from the center to the mass) and curl them towards →V (the direction of motion).
- Your thumb will then point in the direction of →L.
Since →R and →V are both in the plane of rotation, the angular momentum →L will be directed perpendicular to this plane. Therefore, the angular momentum is directed along the axis of rotation.
Based on the analysis, the correct option is:
d) the axis of rotation.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ROLLING MOTION
16 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - HOTS HIGHER ORDER THINKING SKILL
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - DYNAMICS OF ROTATIONAL MOTION ABOUT A FIXED AXIS
10 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions
150 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
A particle of mass m is rotating in a plane in circular path of radius r. Its angular momentum is L. The centripetal force acting on the particle is
View SolutionA particle of-mass m moves along a circular path of radius r with velocity v. What is its instantaneous angular momentum about a point on the plane of the orbit at a distance x from the centre of the axis of rotation.
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionA wire is bent to form a semi-circle of radius a. the wire rotates about its one end with angular velocity ω.Axis of rotation being perpendicular to plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the axis of rotation as shown . The correct statement is :
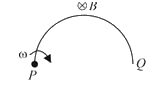
View SolutionAngular momentum of a rigid body rotating about a fixed Axis with angular velocity →ω
View SolutionA wire is bent to form a semi-circle of radius a. The wire rotates about its one end with angular velocity ω. Axis of rotation being perpendicular to plane of the semicircle. In the space, a uniform magnetic field of induction exists along the axis of rotation as shown. The correct statement is
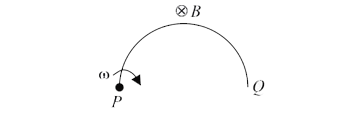
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View Solutionif the earth is treated as a sphere of radius R and mass M, Its angular momentum about the axis of its rotation with period T, is
View SolutionConsider a cylinder rolling on a horizontal plane. Its linear velocity is v and rotational angular velocity is ω. Find its angular momentum about point P on the ground as shown in Fig. What happens to this angular momentum if the cylinder is rotating in opposite direction but moving translationally in the same direction.

View SolutionA body is rotating with angular momentum L. If I is its moment of inertia about the axis of rotation is I, its kinetic energy of rotation is
View Solution
