Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed →V along parallel lines. At a particular instant, →r1 and →r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Which of the following is the correct statement ?
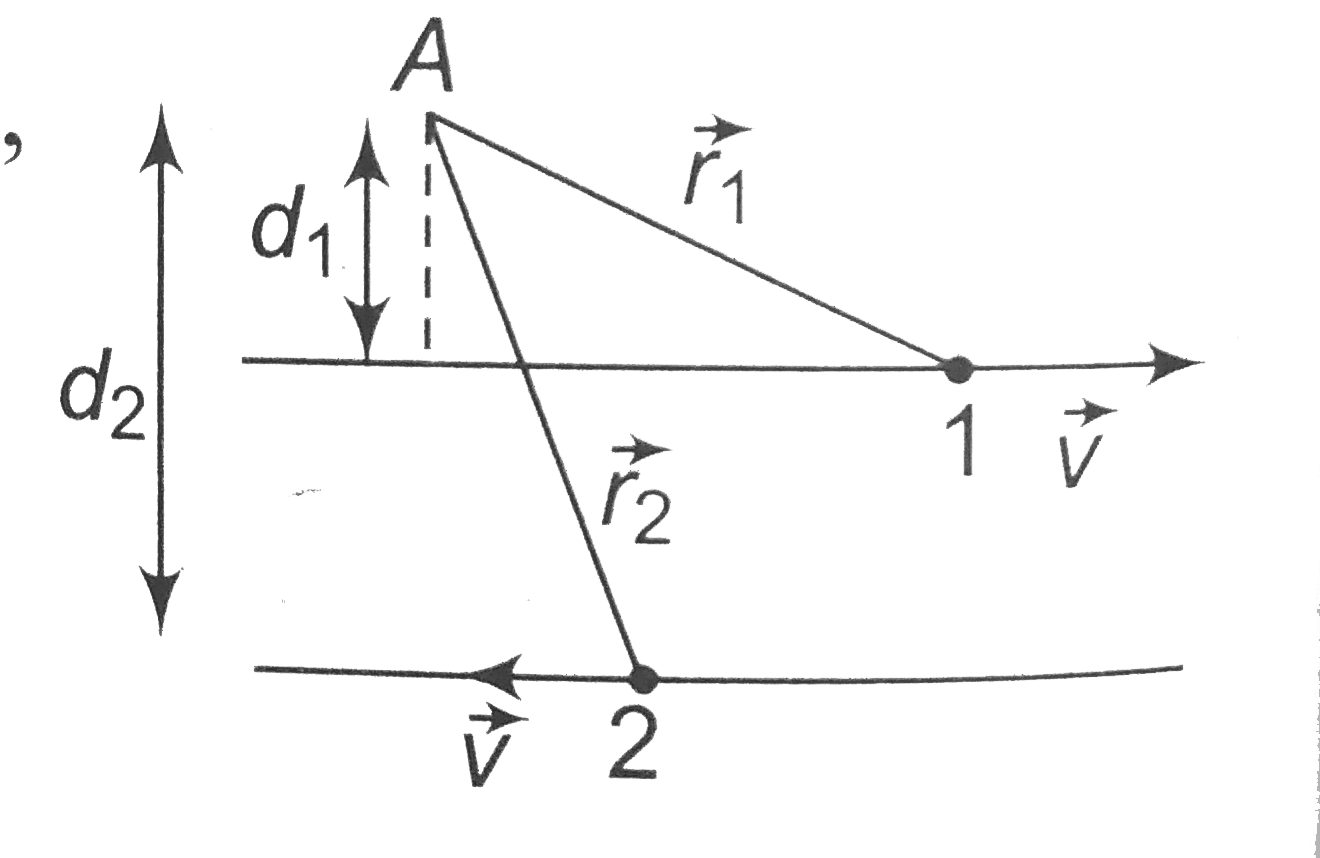 .
.
Angular momentum →L1 of a particle 1 about A is →L1=mv→r1⊙
Angular momentum →L2 of particle 2 about A is →L2=mv→r2⊙
Total angular momentum of the system about A is →L=mv(→r1+→r2)⊙
Total angular momentum of the system about A is →L=mv(d2−d1)⊗
⊗ represents a unit vector going into the page, ⊙ represent a unit vector coming out of the page
The correct Answer is:d
Angular momenum of particle 1 about a is →L1=mvd1
Angular momentum of particle 2 about A is
→L2=mvd2
∴ Total angular momentum of the system about A is
→L=→L2−→L1 (∴L1 and L2 are in opposite directions)
→L=mv(d2−d1)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ROLLING MOTION
16 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - HOTS HIGHER ORDER THINKING SKILL
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - DYNAMICS OF ROTATIONAL MOTION ABOUT A FIXED AXIS
10 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions
150 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
P and Q are two points with position vectors 3→a−2→b and →a+→b respectively. Write the position vector of a point R which divides the line segment PQ in the ratio 2:1 externally.
View SolutionTwo particles each of mass m and speed v, travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.
View SolutionTwo particles each of mass m and speed v, travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.
View SolutionIf →a,→b are the position vectors of the points (1,−1),(−2,m), find the value of m for which →a and →b are collinear.
View SolutionTwo particles undergo SHM along parallel lines with the same time period (T) and equal amplitudes. At particular instant, one particle is at its extreme position while the other is at its mean position. The move in the same direction. They will cross each other after a further time.
View SolutionFind the position vector of a point which divides the join of points with position vectors →a−2→b and 2→a+→b externally in the ratio 2:1.
View SolutionTwo point masses 1 and 2 move with uniform velocities →v1 and →v2, respectively. Their initial position vectors are →r1 and →r2, respectively. Which of the following should be satisfied for the collision of the point masses?
View SolutionIf →r1,→r2,→r3 are the position vectors of the collinear points and scalar pandq exist such that →r3=p→r1+q→r2, then show that p+q=1.
View SolutionIf →r1,→r2,→r3 are the position vectors off thee collinear points and scalar pandq exist such that →r3=p→r1+q→r2, then show that p+q=1.
View SolutionStatement 1: If ∣∣→a+→b∣∣=∣∣→a−→b∣∣, then →a and →b are perpendicular to each other. Statement 2: If the diagonal of a parallelogram are equal magnitude, then the parallelogram is a rectangle. Which of the following Statements is/are correct ?
View Solution
