Two plane mirrors are placed parallel to each other at a distance L apart. A point object O placed between them, at a distance L/3 from one mirror. Both mirrors form multiple image. The distance between any two images cannot be
3L2
2L3
2L
L
The correct Answer is:A
To solve the problem, we will analyze the situation with two parallel mirrors and the multiple images formed by a point object placed between them.
1. Understanding the Setup:
- We have two plane mirrors (let's call them M1 and M2) placed parallel to each other at a distance L apart.
- A point object O is placed between these mirrors at a distance of L3 from mirror M1.
2. Positioning the Object:
- Let’s denote the position of the object O as O.
- The distance from O to M1 is L3.
- Therefore, the distance from O to M2 is L−L3=2L3.
3. Finding the Images:
- The first image O1 formed by mirror M1 will be at a distance L3 from M1, which means it is located at the same distance on the opposite side of M1.
- The second image O2 formed by mirror M2 will be at a distance 2L3 from M2, which is the same as L−L3=2L3 from M1.
4. Calculating Distances Between Images:
- The distance between the first image O1 and the second image O2 is:
Distance(O1,O2)=(L3+2L3)=L
5. Continuing to Find More Images:
- The third image O3 will be the reflection of O1 in M2, which is located at:
Distance from M2=L3+L=4L3
- The fourth image O4 will be the reflection of O2 in M1, which is located at:
Distance from M1=2L3+L=5L3
6. Calculating Distances Between Other Images:
- The distance between O3 and O4 can be calculated as:
Distance(O3,O4)=(5L3−4L3)=L3
7. Identifying Distances That Cannot Occur:
- We have calculated the distances between various images:
- O1 to O2: L
- O3 to O4: L3
- Other combinations yield distances of 2L and 2L3.
- However, the distance 3L2 does not appear in any of the calculations.
Conclusion:
The distance between any two images cannot be 3L2.
- We have two plane mirrors (let's call them M1 and M2) placed parallel to each other at a distance L apart.
- A point object O is placed between these mirrors at a distance of L3 from mirror M1.
- Let’s denote the position of the object O as O.
- The distance from O to M1 is L3.
- Therefore, the distance from O to M2 is L−L3=2L3.
- The first image O1 formed by mirror M1 will be at a distance L3 from M1, which means it is located at the same distance on the opposite side of M1.
- The second image O2 formed by mirror M2 will be at a distance 2L3 from M2, which is the same as L−L3=2L3 from M1.
- The distance between the first image O1 and the second image O2 is:
Distance(O1,O2)=(L3+2L3)=L
- The third image O3 will be the reflection of O1 in M2, which is located at:
Distance from M2=L3+L=4L3
- The fourth image O4 will be the reflection of O2 in M1, which is located at:
Distance from M1=2L3+L=5L3
- The distance between O3 and O4 can be calculated as:
Distance(O3,O4)=(5L3−4L3)=L3
- We have calculated the distances between various images:
- O1 to O2: L
- O3 to O4: L3
- Other combinations yield distances of 2L and 2L3.
- However, the distance 3L2 does not appear in any of the calculations.
The distance between any two images cannot be 3L2.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection Of Light By Spherical Mirrors
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
When the two plane mirror are parallel to each other, then the number of images of an object placed between them is
View SolutionTwo plane mirrors are placed parallel to each other. The distance between the mirrors is 10cm. An object is placed between the mirrors at a distance of 4cm from one of them, say M1. What is the distance between the first time formed at M1 and the second image formed at M2 ?
View SolutionTwo plane mirror are inclined at an angle of 72∘. The number of images of a point object placed between them will be
View SolutionTwo plane mirrors are kept parallel at 20 cm from each other. A point object O is placed exactly in between them. Calculate distance between second images formed by two mirros.

View SolutionTwo plane mirrors are plaved parallel to each other and 40 cm apart. An a object is placed 10 cm from one mirror .What is the distance from the object to the image for each of the five images that are closest to the object?
View SolutionThe figure shows two plane mirrors parallel to each other and an object O placed between them. Then , the distances of the first three images from the mirror M2 will be (in cm)
View SolutionTwo plane mirrors are at 45∘ to each other. If an object is placed between them than the number of images will be
View SolutionYou are standing at a distance 2 metre from a plane mirror.
What is the distance between you and your image ?
View Solutiontwo plane mirror L1andL2 are parallel to each other and 3m apart. A person standing x m from the right mirror L2 looks into this mirror and sees a series of images, The distance between the first and second image is 4 m. Then, the value of x is
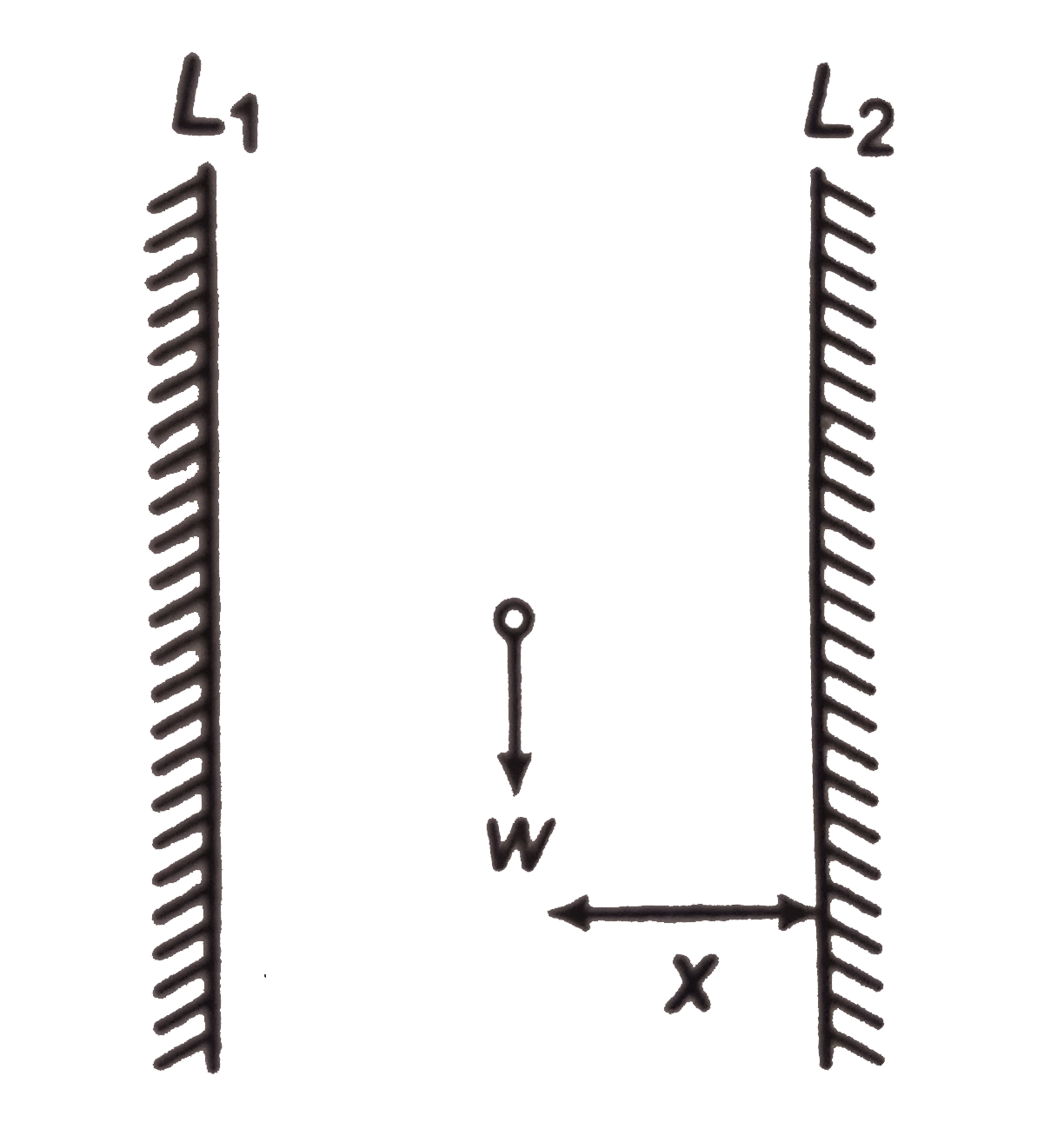
View SolutionTwo plane mirrors are placed at some angle. There are five images formed when an object is placed symmetrically between them . Find the angle between the mirrors.
View Solution
