A magnetic dipole is under the influence of two magnetic fields. The angle between the field direction is 60∘ and one of the fields has magnitude of 1.2×10−2T. If the dipole comes to stable equilibrium at an angle of 30∘ with this Held, then the magnitude of the field is
1.2×10−4T
2.4×10−4T
1.2×10−2T
2.4×10−2T
The correct Answer is:C
To solve the problem of finding the magnitude of the second magnetic field when a magnetic dipole is under the influence of two magnetic fields, we can follow these steps:
1. Understanding the Problem:
We have a magnetic dipole in two magnetic fields, with one field having a magnitude of B1=1.2×10−2T and the angle between the two fields being 60∘. The dipole is in stable equilibrium at an angle of 30∘ with respect to one of the fields.
2. Using Torque Equation:
The torque τ experienced by a magnetic dipole in a magnetic field is given by:
τ=→m×→B
where →m is the magnetic moment and →B is the magnetic field.
3. Condition for Stable Equilibrium:
For stable equilibrium, the net torque must be zero. This occurs when the potential energy is minimized. The potential energy U of a magnetic dipole in a magnetic field is given by:
U=−→m⋅→B
The condition for equilibrium can be expressed as:
mB1sin(30∘)=mB2sin(60∘)
Here, B2 is the magnitude of the second magnetic field.
4. Substituting Values:
We know:
- sin(30∘)=12
- sin(60∘)=√32
Substituting these values into the equation gives:
mB1⋅12=mB2⋅√32
5. Canceling m:
Since m appears on both sides, we can cancel it out (assuming m≠0):
B1⋅12=B2⋅√32
6. Solving for B2:
Rearranging the equation to solve for B2:
B2=B1√3
7. Substituting B1:
Now substituting B1=1.2×10−2T:
B2=1.2×10−2√3≈1.2×10−21.732≈6.93×10−3T
Final Answer:
The magnitude of the second magnetic field B2 is approximately 6.93×10−3T.
We have a magnetic dipole in two magnetic fields, with one field having a magnitude of B1=1.2×10−2T and the angle between the two fields being 60∘. The dipole is in stable equilibrium at an angle of 30∘ with respect to one of the fields.
The torque τ experienced by a magnetic dipole in a magnetic field is given by:
τ=→m×→B
where →m is the magnetic moment and →B is the magnetic field.
For stable equilibrium, the net torque must be zero. This occurs when the potential energy is minimized. The potential energy U of a magnetic dipole in a magnetic field is given by:
U=−→m⋅→B
The condition for equilibrium can be expressed as:
mB1sin(30∘)=mB2sin(60∘)
Here, B2 is the magnitude of the second magnetic field.
We know:
- sin(30∘)=12
- sin(60∘)=√32
mB1⋅12=mB2⋅√32
Since m appears on both sides, we can cancel it out (assuming m≠0):
B1⋅12=B2⋅√32
Rearranging the equation to solve for B2:
B2=B1√3
Now substituting B1=1.2×10−2T:
B2=1.2×10−2√3≈1.2×10−21.732≈6.93×10−3T
The magnitude of the second magnetic field B2 is approximately 6.93×10−3T.
Topper's Solved these Questions
- MAGNETISM AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:MAGNETISM AND MATTER Exercise:MAGNETISM AND GAUSS S LAW
Explore 2 Videos
- MAGNETISM AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:MAGNETISM AND MATTER Exercise:THE EARTH S MAGNETISM
Explore 19 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:NCERT FINGERTPS ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Assertion And Reason
Explore 15 Videos
- MOVING CHARGES AND MAGNETISM Book:NCERT FINGERTPS ENGLISHChapter:MOVING CHARGES AND MAGNETISM Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
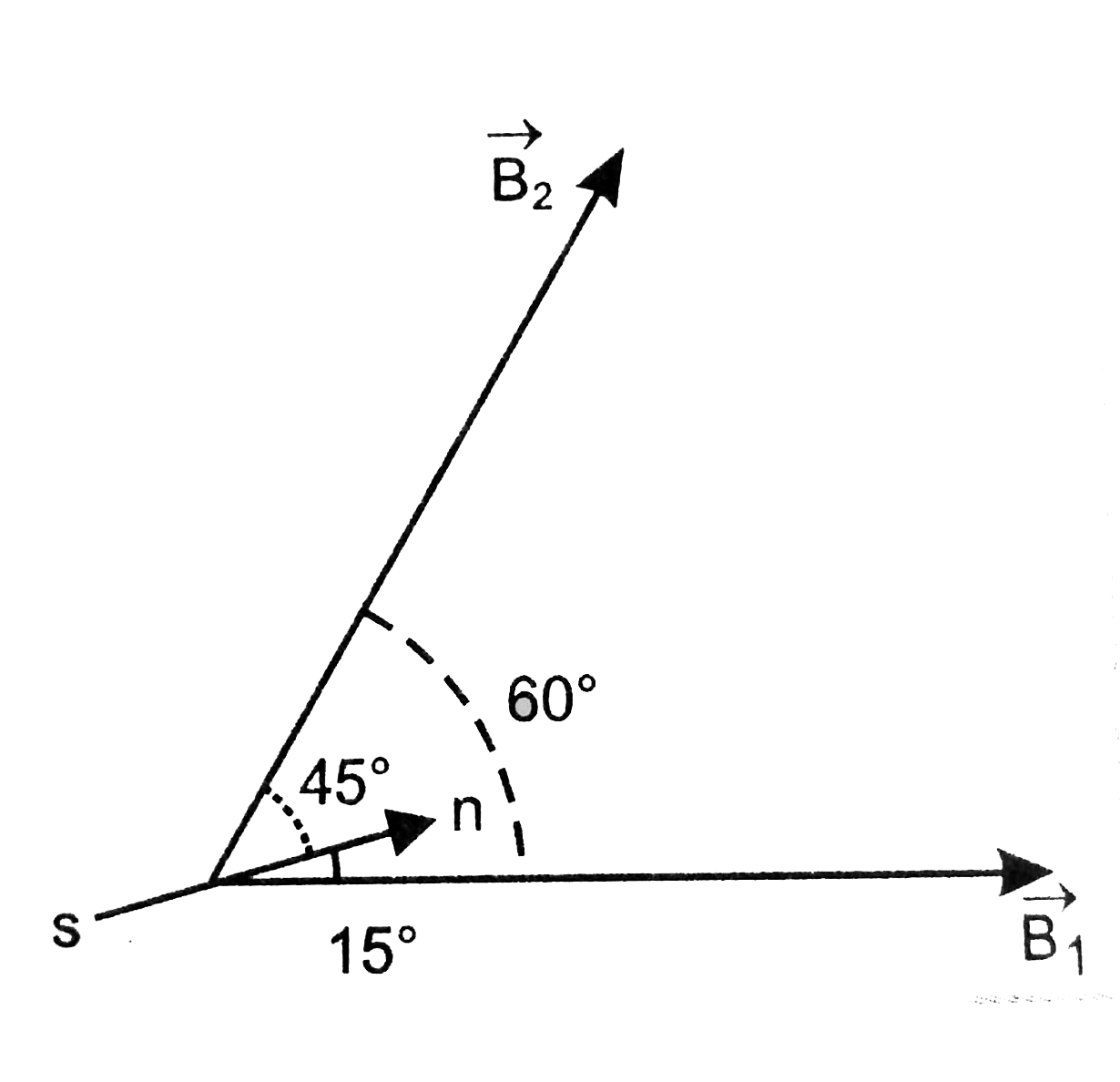
A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is 60∘ and one of the fields has a magnitude of 1⋅2×10−2 tesla. If the dipole comes to stable equilibrium at an angle of 15∘ with this field, figure, what is the magnitude of the other field?
View SolutionA magnetic dipole is acted upon by two magnetic fields with inclined to each other at an angle of 75∘. One of the fields has a magnitude of 15 mT. The dipole attains stable equilibrium at an angle of 30∘ with this field. The magnitude of the other field (in mT) is close to
View SolutionA magentic dipole in a constant magnetic field has
View SolutionA magentic dipole in a constant magnetic field has
View SolutionThe force exerted on a current-carrying wire placed in magnetic field is zero when the angle between the wire and the direction of magnetic field is :
View SolutionAn electric dipole is plced at an angle of 30∘ to a nonuniform electric field. The dipole will experience
View SolutionAn electric dipole is placed at an angle of 30∘ to a non-uniform electric field. The dipole will experience
View SolutionA magnetic dipole is placed in a uniform magnetic field of intensity B, oriented along the direction of the field. If the magnetic dipole moment is M, then the maximum work an external agent can perform in rotating the dipole will be
View SolutionAn electric dipole when placed in uniform electric field has zero potential energy. The angle between dipole moment and electric field is ....
View SolutionAn electric dipole when placed in uniform electric field has zero potential energy. The angle between dipole moment and electric field is ....
View Solution

