When light of wavelength 400nm is incident on the cathode of photocell, the stopping potential recorded is 6V. If the wavelength of the incident light is to 600nm, calculate the new stopping potential. [Given h=6.6×10−34Js,c=3×108m/s,e=1.6×10−19C]
1.03V
2.42V
4.97V
3.58V
The correct Answer is:C
To solve the problem, we will use Einstein's photoelectric equation, which relates the energy of the incident photons to the stopping potential in a photocell. The equation is given as:
eV=hcλ−W0
where:
- e is the charge of an electron,
- V is the stopping potential,
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the incident light,
- W0 is the work function of the material.
Step 1: Write down the given values
From the problem:
- For the first wavelength (λ1=400nm=400×10−9m):
- Stopping potential (V1=6V)
- For the second wavelength (λ2=600nm=600×10−9m):
- We need to find V2.
Step 2: Write the equations for both wavelengths
Using the photoelectric equation for both wavelengths, we have:
1. For λ1:
eV1=hcλ1−W0
e(6)=(6.6×10−34)(3×108)400×10−9−W0
2. For λ2:
eV2=hcλ2−W0
eV2=(6.6×10−34)(3×108)600×10−9−W0
Step 3: Subtract the two equations
By subtracting the two equations, we eliminate W0:
eV1−eV2=(hcλ1−W0)−(hcλ2−W0)
This simplifies to:
e(V1−V2)=hcλ1−hcλ2
Step 4: Rearranging the equation
Rearranging gives us:
V2=V1−hce(1λ1−1λ2)
Step 5: Substitute the known values
Now, substitute the known values into the equation:
- h=6.6×10−34Js
- c=3×108m/s
- e=1.6×10−19C
- λ1=400×10−9m
- λ2=600×10−9m
- V1=6V
Calculating hce:
hce=(6.6×10−34)(3×108)1.6×10−19≈1.237×10−6V m
Now, substituting into the equation for V2:
V2=6−(1.237×10−6)(1400×10−9−1600×10−9)
Calculating the term in parentheses:
1400×10−9−1600×10−9=600−400240000=200240000=11200
Thus:
V2=6−(1.237×10−6×11200)
Calculating 1.237×10−6×11200:
≈1.031×10−9V
Finally, calculating V2:
V2≈6−0.00497≈4.97V
Final Answer:
The new stopping potential V2 is approximately 4.97 V.
---
- e is the charge of an electron,
- V is the stopping potential,
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the incident light,
- W0 is the work function of the material.
From the problem:
- For the first wavelength (λ1=400nm=400×10−9m):
- Stopping potential (V1=6V)
- For the second wavelength (λ2=600nm=600×10−9m):
- We need to find V2.
Using the photoelectric equation for both wavelengths, we have:
eV1=hcλ1−W0
e(6)=(6.6×10−34)(3×108)400×10−9−W0
eV2=hcλ2−W0
eV2=(6.6×10−34)(3×108)600×10−9−W0
By subtracting the two equations, we eliminate W0:
Rearranging gives us:
Now, substitute the known values into the equation:
- c=3×108m/s
- e=1.6×10−19C
- λ1=400×10−9m
- λ2=600×10−9m
- V1=6V
The new stopping potential V2 is approximately 4.97 V.
Topper's Solved these Questions
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Paper 1
Explore 50 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Paper 2
Explore 50 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Papper 2
Explore 50 Videos
- NUCLEIBook:NCERT FINGERTPS ENGLISHChapter:NUCLEIExercise:Assertion And Reason
Explore 15 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:NCERT Exemplar
Explore 11 Videos
Similar Questions
When light of wavelength λ is incident on photosensitive surface, the stopping potential is V. When light of wavelength 3λ is incident on same surface, the stopping potential is V6 Threshold wavelength for the surface is
View SolutionCalculate the (a) momentum and (b) de-Broglie wavelength of the electrons accelerated through a potential difference of 56V. Given, h=6.63×10−34Js,me=9.1×10−31kg,e=1.6×10−19C.
View Solution
Knowledge Check
The work function of Cs is 2.14 ev find the wavelength of the incident light if the stopping potential is 0.6 V.
A326 nmB454 nmC524 nmD232 nmThe de Broglie wavelength of an electron with kinetic energy 120 e V is (Given h=6.63×10−34Js,me=9×10−31kg,1eV=1.6×10−19J)
A2.13Ã…B1.13Ã…C4.15Ã…D3.14Ã…
If de Broglie wavelength of an electron is 0.5467 Å,
find the kinetic energy of electron in eV. Given h=6.6×10−34 Js ,
e=1.6×10−19 C, me=9.11×10−31 kg.
View SolutionThe work function of cesium is 2.14 eV. Find (a) the threshold frequency for cesium, and (b) the wavelength of the incident light if the photo current is brought to zero by a stopping potential 0.60 V. Given h=6.63×10−34Js.
View SolutionMonochromatic light of wavelength 198 nm is incident on the surface of a metal, whose work function is 2.5 eV. Calculate the stopping potential.
View SolutionIn a photoelectric experiment, it was found that the stopping potential decreases from 1.85 V to 0.82 V as the wavelength of the incident light is varied from 300nm to 400nm. Calculate the value of the Planck constant from these data.
View SolutionThe voltage applied to an X-ray tube is 20 kV. The minimum wavelength of X-ray produced, is given by 31×n50Å then n will be
(h=6.62×10−34Jx,c=3×108m/s,e=1.6×10−19 coulomb):
View SolutionIn a historical experiment to determine Planck's constant, a metal surface was irradiated with light of different wavelengths. The emitted photoelectron energies were measured by applying a stopping potential. The relevant data for the wavelength (λ). ) of incident light and the corresponding stopping potential (V0) are given below :
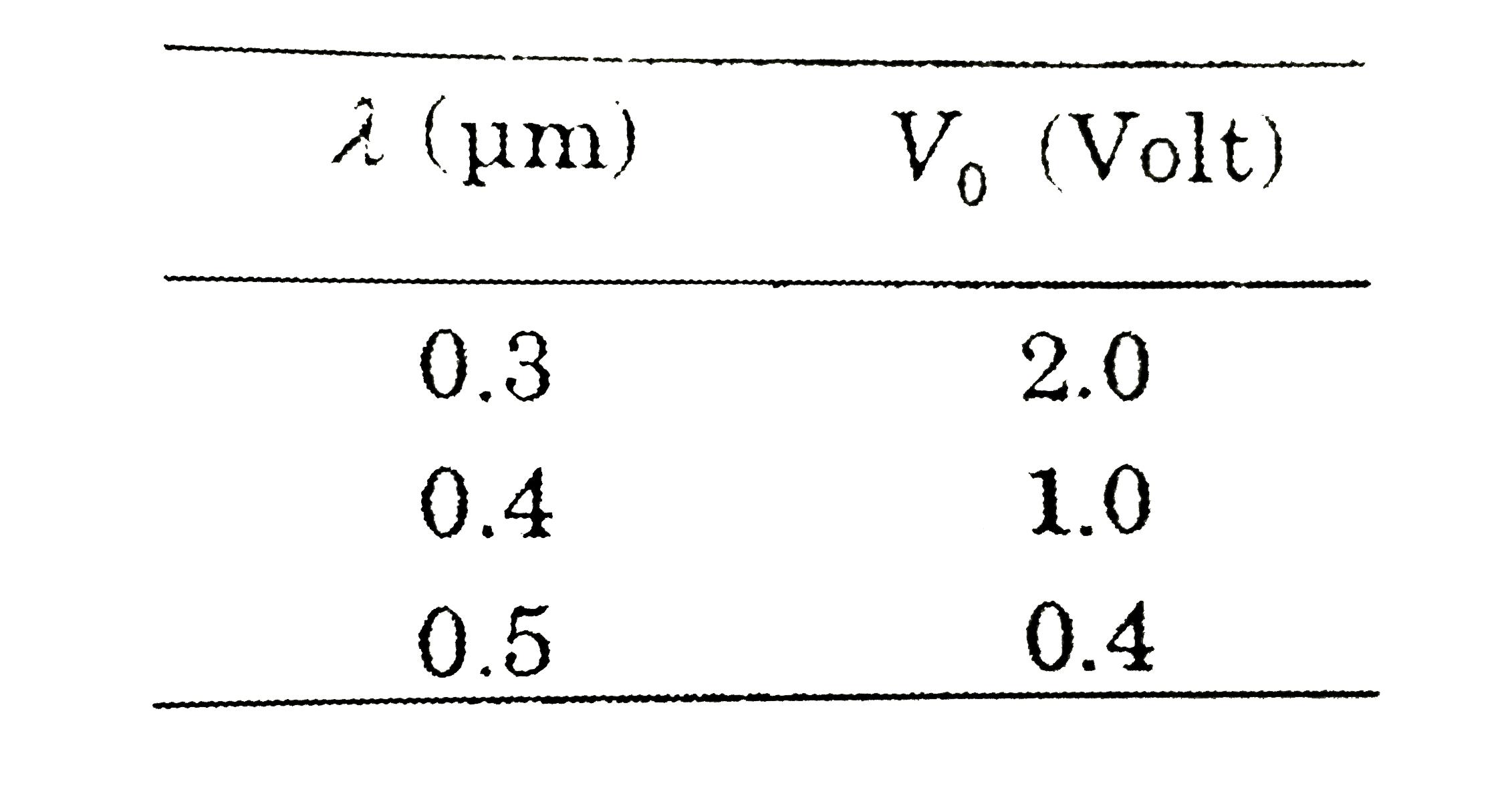
Given that c=3×108ms−1ande=1.6×10−19C Planck's constant (in units of J s) found from such an experiment is
View Solution

