In a historical experiment to determine Planck's constant, a metal surface was irradiated with light of different wavelengths. The emitted photoelectron energies were measured by applying a stopping potential. The relevant data for the wavelength (λ). ) of incident light and the corresponding stopping potential (V0) are given below :
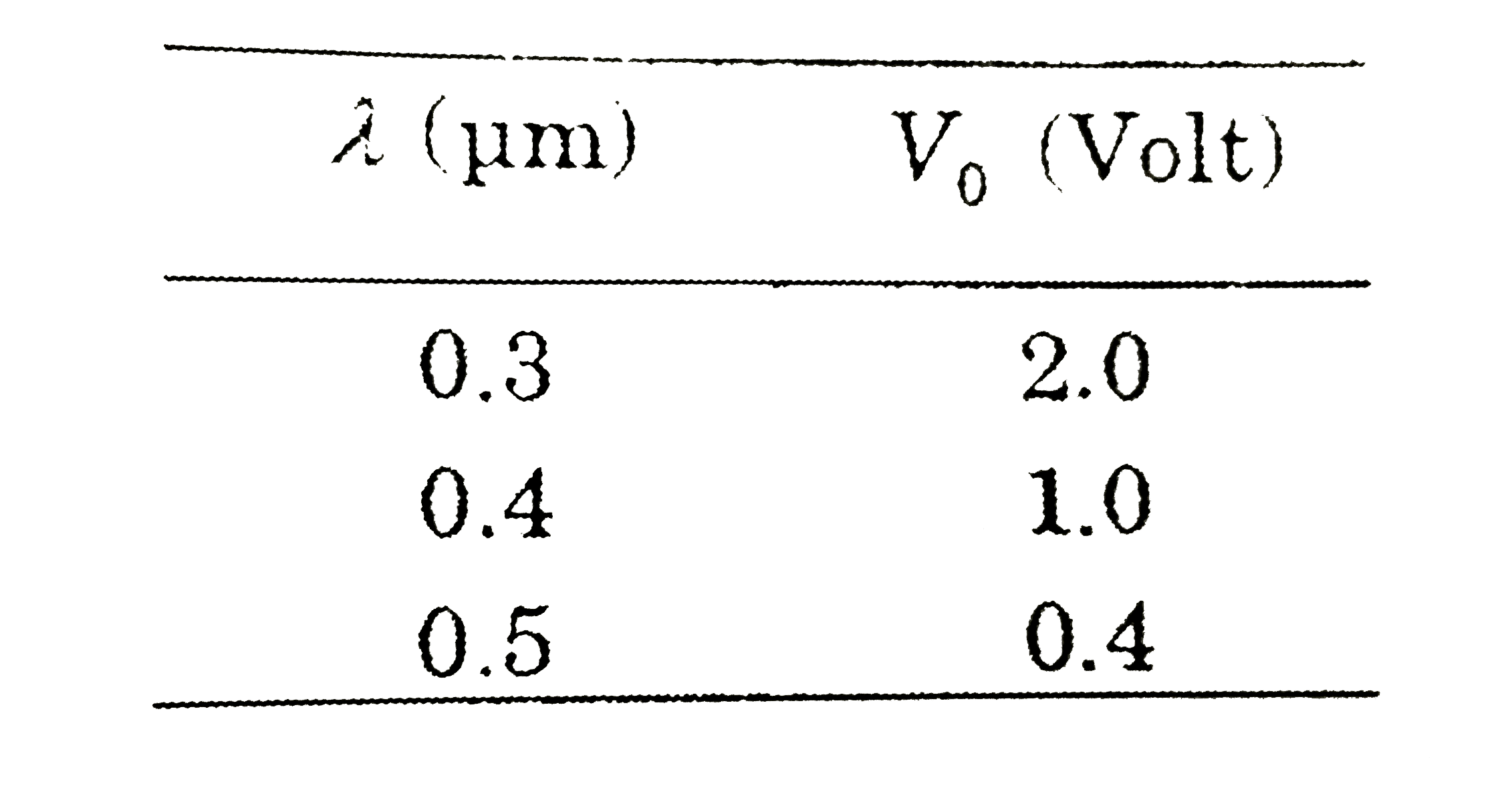
In a historical experiment to determine Planck's constant, a metal surface was irradiated with light of different wavelengths. The emitted photoelectron energies were measured by applying a stopping potential. The relevant data for the wavelength (lambda). ) of incident light and the corresponding stopping potential (V0 ) are given below : Given that c=3xx10^8ms^(-1) and e=1.6xx10^(-19)C Planck's constant (in units of J s) found from such an experiment is
Given that c=3×108ms−1ande=1.6×10−19C Planck's constant (in units of J s) found from such an experiment is

A

6.0×10−34

B

6.4×10−34

C

6.6×10−34

D

6.8×10−34

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

KEmax=hCλ−ϕ
eVs=hCλ−ϕ
1.6×10−19×2=h×3×1083000×10−10−ϕ.....(i)
1.6×10−19×1=h×3×1084000×10−10−ϕ......(ii)
From (ii) ϕ=h×3×1084000×10−10−1.6×10−19
1.6×10−19×2=h×3×1083000×10−10−h×3×1084000×10−10+1.6×10−19
1.6×10−19=h×3×10810−7(13−14)=h×3×10810−7[4−312]
1.6×10−19=h×3×10810−7×112
1.6×4×10−19×10−7108=h
6.4×10−34Js=h

Updated on:21/07/2023
|
Class 12PHYSICSSIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • When light of wavelength 400nm is incident on the cathode of photocell, the stopping potential recorded is 6V. If the wavelength of the incident light is to 600nm, calculate the new stopping potential. [Given h=6.6×10−34Js,c=3×108m/s,e=1.6×10−19C]

    A1.03V
    B2.42V
    C4.97V
    D3.58V