Electric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
ql
√3ql
zero
4ql
The correct Answer is:B
To find the magnitude of the electric dipole moment of the system with charges q,q,−2q placed at the corners of an equilateral triangle ABC of side l, we can follow these steps:
Step 1: Understand the Configuration
We have an equilateral triangle ABC with:
- Charge q at point A,
- Charge q at point B,
- Charge −2q at point C.
Step 2: Define the Dipole Moment
The electric dipole moment →p for a system of charges is defined as:
→p=∑→pi=∑qi→ri
where qi is the charge and →ri is the position vector of the charge from the origin.
Step 3: Calculate Individual Dipole Moments
We can calculate the dipole moments due to each charge with respect to a reference point (let's take point C as the origin):
- For charge q at A (distance l):
→pA=q⋅l^rAC
- For charge q at B (distance l):
→pB=q⋅l^rBC
- For charge −2q at C (which we consider as the origin, so its contribution is zero):
→pC=−2q⋅0=0
Step 4: Determine the Direction of Dipole Moments
The dipole moments →pA and →pB will have a certain angle between them. Since triangle ABC is equilateral, the angle between →pA and →pB is 60∘.
Step 5: Calculate the Resultant Dipole Moment
Using the formula for the resultant of two vectors:
|→pnet|=√|→pA|2+|→pB|2+2|→pA||→pB|cos(60∘)
Substituting |→pA|=ql and |→pB|=ql:
|→pnet|=√(ql)2+(ql)2+2(ql)(ql)⋅12
=√(ql)2+(ql)2+(ql)2=√3(ql)2=√3ql
Final Answer
Thus, the magnitude of the electric dipole moment of the system is:
|→pnet|=√3ql
We have an equilateral triangle ABC with:
- Charge q at point A,
- Charge q at point B,
- Charge −2q at point C.
The electric dipole moment →p for a system of charges is defined as:
→p=∑→pi=∑qi→ri
where qi is the charge and →ri is the position vector of the charge from the origin.
We can calculate the dipole moments due to each charge with respect to a reference point (let's take point C as the origin):
- For charge q at A (distance l):
→pA=q⋅l^rAC
- For charge q at B (distance l):
→pB=q⋅l^rBC
- For charge −2q at C (which we consider as the origin, so its contribution is zero):
→pC=−2q⋅0=0
The dipole moments →pA and →pB will have a certain angle between them. Since triangle ABC is equilateral, the angle between →pA and →pB is 60∘.
Using the formula for the resultant of two vectors:
|→pnet|=√|→pA|2+|→pB|2+2|→pA||→pB|cos(60∘)
Substituting |→pA|=ql and |→pB|=ql:
|→pnet|=√(ql)2+(ql)2+2(ql)(ql)⋅12
=√(ql)2+(ql)2+(ql)2=√3(ql)2=√3ql
Thus, the magnitude of the electric dipole moment of the system is:
|→pnet|=√3ql
Topper's Solved these Questions
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Papper 2
Explore 50 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Papper 3
Explore 50 Videos
- NUCLEIBook:NCERT FINGERTPS ENGLISHChapter:NUCLEIExercise:Assertion And Reason
Explore 15 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:NCERT Exemplar
Explore 11 Videos
Similar Questions
Three point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is ?
View SolutionEqual charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View SolutionConsider three charges q,−q, (in Sl units) at the vetrices of an equilateral triangle with side length b. The magnitude of electric field at the centroid of the triangle is :
View SolutionThree charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
View SolutionFour charge particles of chagres −q,−q,−q and 3q are placed at the vertices of a square of side a as shown. The magnitude of dipole moment of the arrangement is 2n/2 qa where n is ______.

View SolutionThree charges +q, -q and +q are kept at the corners of an equilateral triangle of side d. Find the resultant electric force on a charge +q placed at the centroid O of the triangle.
View SolutionThree identical dipoles with charges q and −q, and separation A between the charges, are placed at the corners of an equilateral triangle of side D as shown in (Fig. 3.123). Find the interaction energy of the system (a<<d).
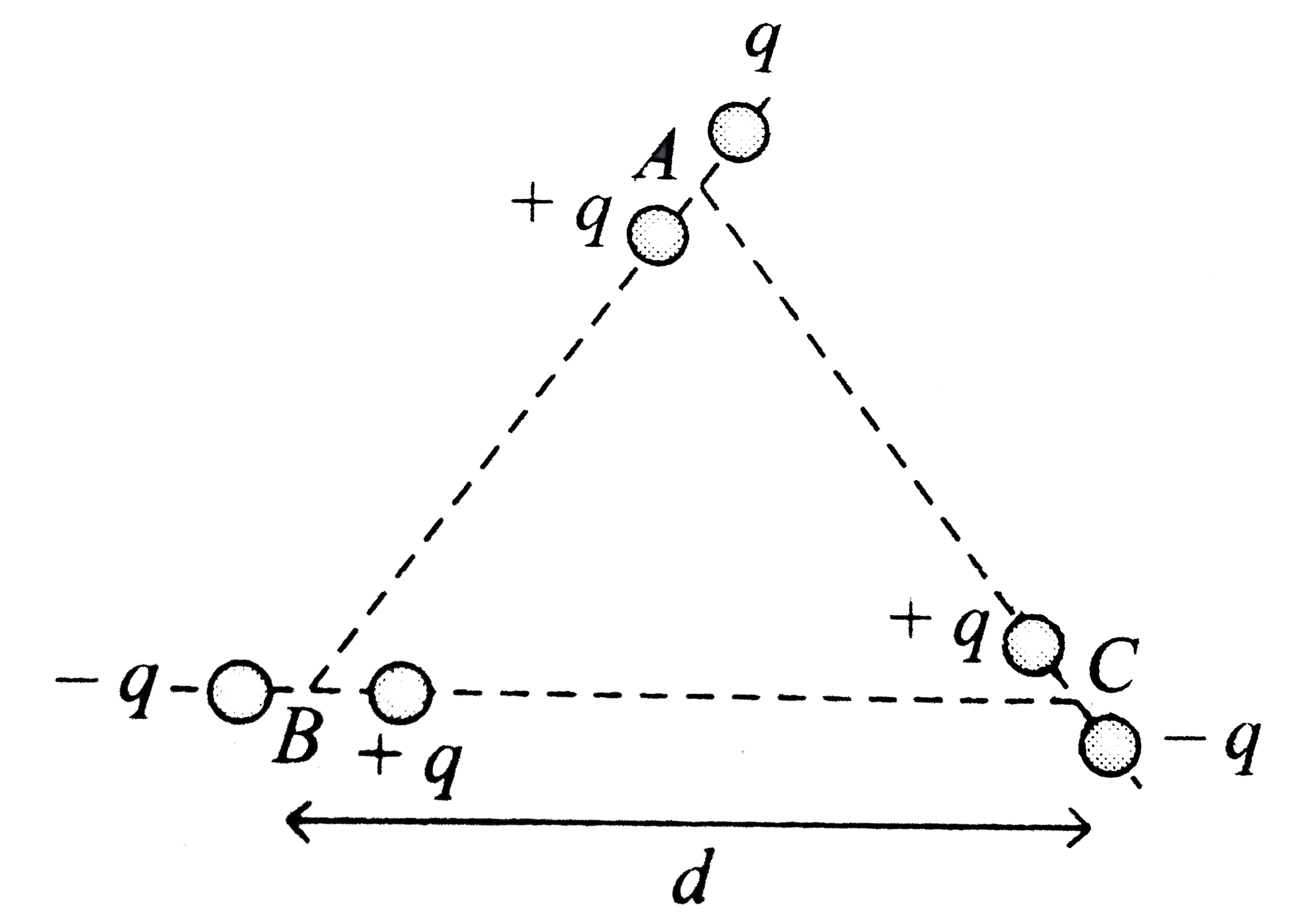 .
.
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View SolutionThree charges +q, +q and -2q are placed at the vertices of an equilareral triagle. What is the dipole moment of the system?
View Solution

