The photoelectric threshold wavelength for silver is λ0. The energy of the electron ejected from the surface of silver by an incident wavelength λ(λ<λ0) will be
hc(λ0−λ)
hcλ0−λ
hc/(λ0−λλλ0)
hc(λ0−λλλ0)
The correct Answer is:D
To find the energy of the electron ejected from the surface of silver by an incident wavelength λ (where λ<λ0), we can use Einstein's photoelectric equation. Here’s the step-by-step solution:
Step 1: Understand the Photoelectric Effect
The photoelectric effect states that when light of a certain frequency (or wavelength) hits a material, it can eject electrons from that material. The energy of the incident light is related to its wavelength.
Step 2: Use Einstein's Photoelectric Equation
Einstein's photoelectric equation is given by:
K.E.=Eincident−ϕ
where:
- K.E. is the kinetic energy of the ejected electron,
- Eincident is the energy of the incident photon,
- ϕ is the work function of the material.
Step 3: Express Energy in Terms of Wavelength
The energy of a photon can be expressed in terms of its wavelength:
Eincident=hcλ
where:
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the incident light.
The work function ϕ can also be expressed in terms of the threshold wavelength λ0:
ϕ=hcλ0
Step 4: Substitute into the Photoelectric Equation
Substituting the expressions for Eincident and ϕ into the photoelectric equation gives:
K.E.=hcλ−hcλ0
Step 5: Factor Out Common Terms
We can factor out hc:
K.E.=hc(1λ−1λ0)
Step 6: Simplify the Expression
To combine the terms in the parentheses, find a common denominator:
K.E.=hc(λ0−λλλ0)
Final Result
Thus, the kinetic energy of the ejected electron is given by:
K.E.=hc(λ0−λ)λλ0
Summary
The energy of the electron ejected from the surface of silver by an incident wavelength λ is:
K.E.=hc(λ0−λ)λλ0
---
The photoelectric effect states that when light of a certain frequency (or wavelength) hits a material, it can eject electrons from that material. The energy of the incident light is related to its wavelength.
Einstein's photoelectric equation is given by:
K.E.=Eincident−ϕ
where:
- K.E. is the kinetic energy of the ejected electron,
- Eincident is the energy of the incident photon,
- ϕ is the work function of the material.
The energy of a photon can be expressed in terms of its wavelength:
Eincident=hcλ
where:
- h is Planck's constant,
- c is the speed of light,
- λ is the wavelength of the incident light.
ϕ=hcλ0
Substituting the expressions for Eincident and ϕ into the photoelectric equation gives:
K.E.=hcλ−hcλ0
We can factor out hc:
K.E.=hc(1λ−1λ0)
To combine the terms in the parentheses, find a common denominator:
K.E.=hc(λ0−λλλ0)
Thus, the kinetic energy of the ejected electron is given by:
K.E.=hc(λ0−λ)λλ0
The energy of the electron ejected from the surface of silver by an incident wavelength λ is:
K.E.=hc(λ0−λ)λλ0
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - PARTICLE NATURE OF LIGHT : THE PHOTON
19 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - WAVE NATURE OF MATTER
37 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - EXPERIMENTAL STUDY OF PHOTOELECTRIC EFFECT
11 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
The photoelectric threshold wavelength of silver is 3250×10−10m. The velocity of the electron ejected from a silver surface by ultraviolet light of wavelength 2536×10−10m is
(Givenh=4.14×106ms−1eVs and c=3×108ms−1)
View SolutionThe photoelectric threshold wavelength of silver is 3250×10−10m. The velocity of the electron ejected from a silver surface by ultraviolet light of wavelength 2536×10−10m is
(Givenh=4.14×106ms−1eVs and c=3×108ms−1)
View SolutionThe photoelectric threshold wavelength of a metal is 300 nm. The maximum kinetic energy of electrons ejected from the metal surface by ultraviolet light of wavelength 250 nm is nearly (givenh=4.14⋅10−15eVsandc=3⋅108ms−1)
View SolutionThe threshold wavelength of a metal is 230nm calculate the KE of the electrons from that metal surface by using UV radiation of wavelength 180nm
View SolutionThe photo electric threshold wavelength for a metal is 2750A∘, The minimum energy of a photon that can produce photoelectric effect in the metal is
View SolutionThe kinetic energy of an electron is E when the incident wavelength is λ To increase ti KE of the electron to 2E, the incident wavelength must be
View Solution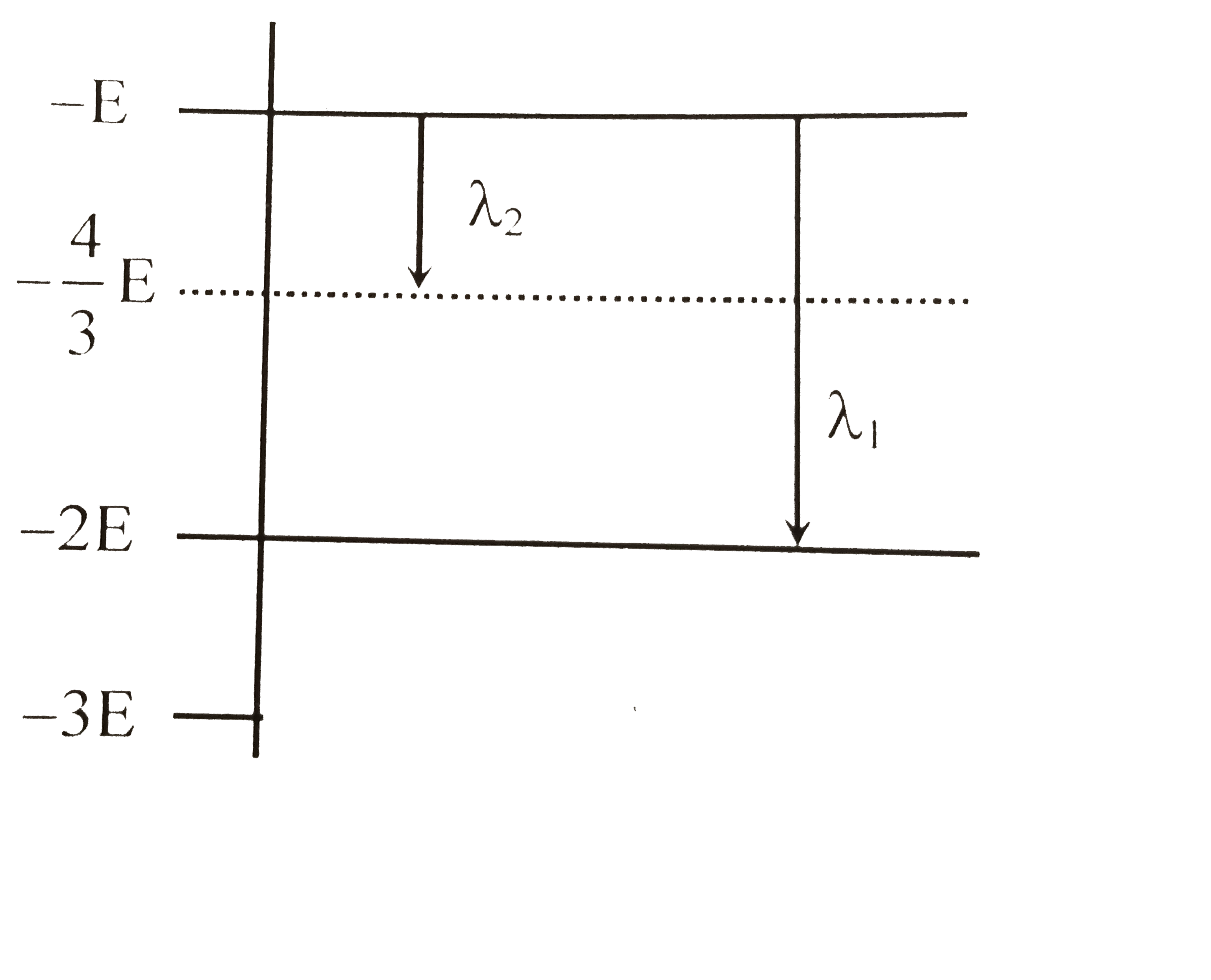
Some energy levels of a molecule are shown in the figure. The ratio of the wavelength r=λ1λ2,is given by:
View SolutionA 40 W ultraviolet light source of wavelength 2480A. Illuminates a magnesium (mg) surface placed 2 m away. Determine the number of photons emitted from the surface per second and the number incident on unit area of Mg surface per second . The photoelectric work function for Mg is 3.68eV. Calculate the kinetic energy of the fastest electrons ejected from the surface. Determine the maximum wavelength for which the photoelectric effects can be observed with Mg surface.
View SolutionIf λoandλ be the threshold wavelength and wavelength of incident light , the velocity of photoelectron ejected from the metal surface is :
View SolutionThe threshold wavelength for ejection of electrons from a metal is 430 nm. The work function for the photoelectric emission from the metal is
View Solution
