A resistor of 500Ω and an inductance of 0.5 H are in series with an ac source which is given by V=100√2sin(1000t). The power factor of the combination is
1√2
1√3
0.5
0.6
The correct Answer is:A
To find the power factor of the given circuit with a resistor and an inductor in series, we can follow these steps:
Step 1: Identify Given Values
- Resistance, R=500Ω
- Inductance, L=0.5H
- Voltage source, V=100√2sin(1000t)
Step 2: Determine Angular Frequency
From the voltage equation, we can identify the angular frequency ω:
- ω=1000rad/s
Step 3: Calculate Inductive Reactance
The inductive reactance XL is given by the formula:
XL=ωL
Substituting the values:
XL=1000×0.5=500Ω
Step 4: Calculate Impedance
The total impedance Z in a series circuit with resistance and inductive reactance is given by:
Z=√R2+X2L
Substituting the values:
Z=√(500)2+(500)2=√250000+250000=√500000=707.1Ω
Step 5: Calculate Power Factor
The power factor cosϕ is defined as:
cosϕ=RZ
Substituting the values:
cosϕ=500707.1≈0.707
Step 6: Conclusion
The power factor of the combination is:
cosϕ≈0.707or1√2
- Resistance, R=500Ω
- Inductance, L=0.5H
- Voltage source, V=100√2sin(1000t)
From the voltage equation, we can identify the angular frequency ω:
- ω=1000rad/s
The inductive reactance XL is given by the formula:
XL=ωL
Substituting the values:
XL=1000×0.5=500Ω
The total impedance Z in a series circuit with resistance and inductive reactance is given by:
Z=√R2+X2L
Substituting the values:
Z=√(500)2+(500)2=√250000+250000=√500000=707.1Ω
The power factor cosϕ is defined as:
cosϕ=RZ
Substituting the values:
cosϕ=500707.1≈0.707
The power factor of the combination is:
cosϕ≈0.707or1√2
Topper's Solved these Questions
- ALTERNATING CURRENT Book:NCERT FINGERTPS ENGLISHChapter:ALTERNATING CURRENT Exercise:HOTS
Explore 8 Videos
- ALTERNATING CURRENT Book:NCERT FINGERTPS ENGLISHChapter:ALTERNATING CURRENT Exercise:NCERT
Explore 7 Videos
- ATOMS Book:NCERT FINGERTPS ENGLISHChapter:ATOMS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A 200Ω resistor and 1H inductor are joined in series with an ac source of emf 10√2sin(200t)V. Calculate the phases difference between emf and current.
View SolutionA coil having a resistance of 50.0Ω and an inductance of 0.500 henry is connected to an AC source of 110 volts, 50.0 cycle/s. Find the rms value of the current in the circuit.
View Solution
Knowledge Check
An inductor 200 mH, capacitor 500μF and resistor 10Ω are connected in series with a 100 V variable frequency ac source. What is the frequency at which the power factor of the circuit is unity?
A10.22HzB12.4HzC19.2HzD15.9Hz
A capacitor of capacitance 2 mF and resistor of resistance 12 Ω are connected in series with voltage source V=(195√2(V))[sin(100rads)t] - The average power dissipated in the circuit will be
View SolutionA capacitor of capacitance 100μF and a coil of resistance 50Ω and inductance 0.5H are connected in series with a110V,50HzAC source. Find the rms value of the current.
View SolutionAn inductor 200 mH, capacitor 500μF, resistor 10 ohm are connected in series with a 100 V, variable frequency a.c. source. Calculate (i) frequency at which power factor of the circuit is unity (ii) current amplitude at this frequency (iii) Q factor.
View SolutionAn inductor 200 mH, capactior 500μF, resistor 10 ohm are connected in series with a 100 V, varialbe frequency a.c. source. Calculate (i) frequency at which power factor of the circuit is unity (ii) current amplitude at this frequency (iii) Q factor.
View SolutionA 20 μF capacitor, 0.2 H inductor and a 50 Ω resistor are connected in series to an a.c. Source whose emf is given by E = 310 sin (314 t) where E is in volt and t is in second. Calculate :
peak value of current in the circuit.
View SolutionA 30 μF capacitor, 0.2 H inductor and a 50 Ω resistor are connected in series to an a.c. Source whose emf is given by E = 310 sin (314 t) where E is in volt and t is in second. Calculate :
The impedance of the circuit and
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
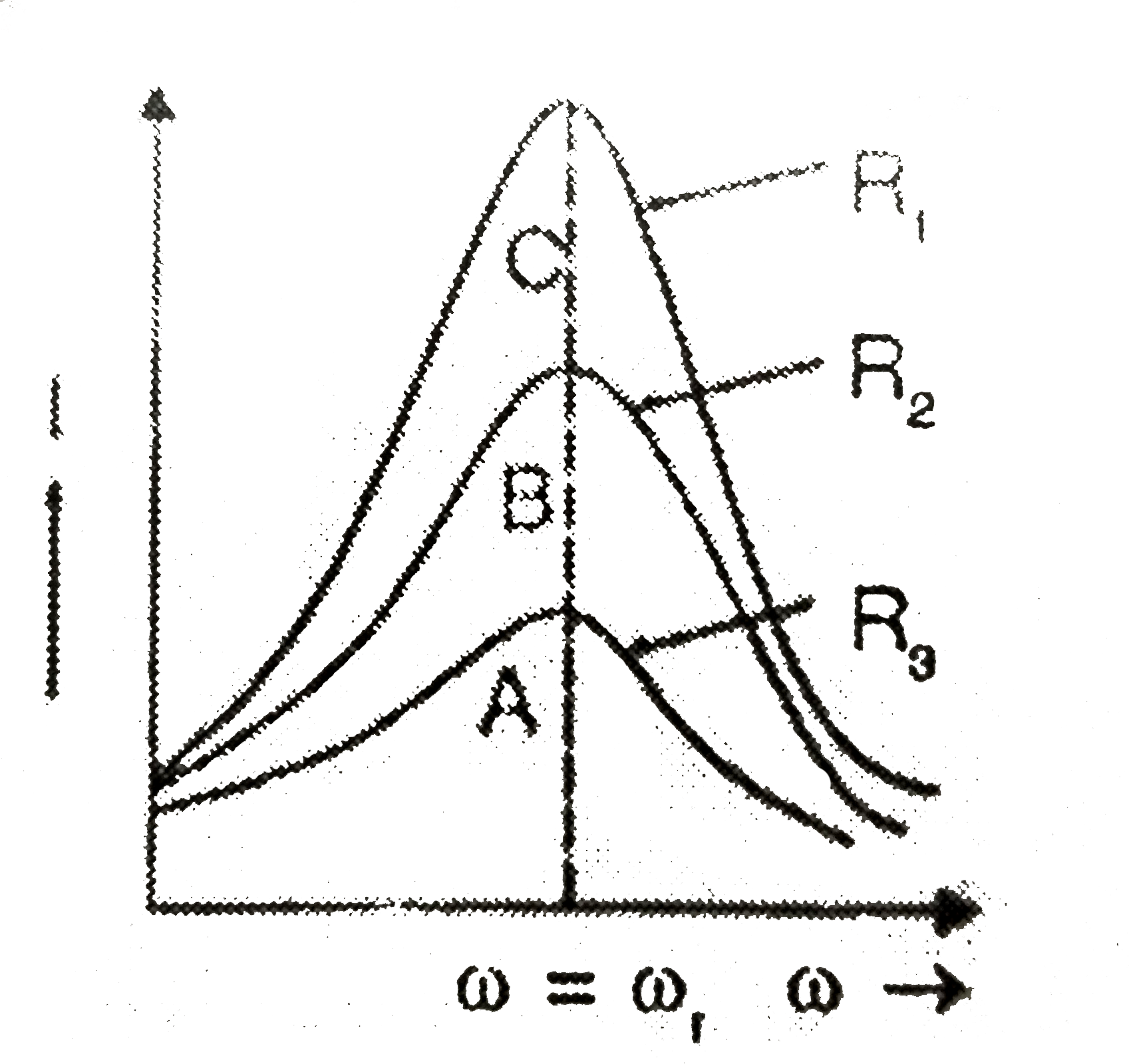
View Solution

