A potentiometer wire of length 100 cm has a resistance of 100Ω it is connected in series with a resistance and a battery of emf 2 V and of negligible internal resistance. A source of emf 10 mV is balanced against a length of 40 cm of the potentiometer wire. what is the value of the external resistance?
790Ω
890Ω
990Ω
1090Ω
The correct Answer is:A
To solve the problem step by step, we will follow the information provided in the question and apply the principles of a potentiometer circuit.
Step 1: Understand the Circuit
We have a potentiometer wire of length 100 cm and resistance 100 Ω connected in series with an external resistance R and a battery of emf 2 V. The internal resistance of the battery is negligible.
Step 2: Determine the Current in the Circuit
The total resistance in the circuit is the sum of the resistance of the potentiometer wire and the external resistance R:
Rtotal=100Ω+R
Using Ohm's Law, the current I in the circuit can be calculated as:
I=VRtotal=2V100Ω+R
Step 3: Calculate the Potential Difference Across the Potentiometer Wire
The potential difference across a length L of the potentiometer wire is proportional to the current and the resistance of that length. The resistance of the 40 cm length of the potentiometer wire can be calculated as:
RL=L100×100Ω=40100×100Ω=40Ω
The potential difference VL across this length is given by:
VL=I×RL=I×40Ω
Step 4: Set the Potential Difference Equal to the Source Emf
According to the problem, this potential difference VL is balanced against a source of emf of 10 mV (or 0.01 V):
I×40Ω=10mV=0.01V
Step 5: Substitute the Expression for Current
Substituting the expression for I from Step 2 into the equation from Step 4:
2V100+R×40=0.01
Step 6: Solve for R
Rearranging the equation gives:
80100+R=0.01
Cross-multiplying yields:
80=0.01×(100+R)
Expanding this gives:
80=1+0.01R
Subtracting 1 from both sides:
79=0.01R
Dividing both sides by 0.01:
R=790.01=7900Ω
Final Answer
The value of the external resistance R is:
7900Ω
We have a potentiometer wire of length 100 cm and resistance 100 Ω connected in series with an external resistance R and a battery of emf 2 V. The internal resistance of the battery is negligible.
The total resistance in the circuit is the sum of the resistance of the potentiometer wire and the external resistance R:
Rtotal=100Ω+R
Using Ohm's Law, the current I in the circuit can be calculated as:
I=VRtotal=2V100Ω+R
The potential difference across a length L of the potentiometer wire is proportional to the current and the resistance of that length. The resistance of the 40 cm length of the potentiometer wire can be calculated as:
RL=L100×100Ω=40100×100Ω=40Ω
The potential difference VL across this length is given by:
VL=I×RL=I×40Ω
According to the problem, this potential difference VL is balanced against a source of emf of 10 mV (or 0.01 V):
I×40Ω=10mV=0.01V
Substituting the expression for I from Step 2 into the equation from Step 4:
2V100+R×40=0.01
Rearranging the equation gives:
80100+R=0.01
Cross-multiplying yields:
80=0.01×(100+R)
Expanding this gives:
80=1+0.01R
Subtracting 1 from both sides:
79=0.01R
Dividing both sides by 0.01:
R=790.01=7900Ω
The value of the external resistance R is:
7900Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:HOTS
Explore 8 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:EXEMPLAR PROBLEMS
Explore 6 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:METER BRIDGE
Explore 4 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTPS ENGLISHChapter:COMMUNITCATION SYSTEMSExercise:Assertion And Reason
Explore 30 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A potentiometer wire of length 100cm having a resistance of 10Ω is connected in series with a resistance R and a cell of emf 2V of negligible internal resistance. A source of emf

of 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of resistance R ?
View SolutionA potentiometer wire of length 100cm having a resistance of 10Ω is connected in series with a resistance R and a cell of emf 2V of negligible internal resistance. A source of emf

of 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of resistance R ?
View Solution
Knowledge Check
A potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance and a cell of emf 2V and of negligible interal resistance. A source of emf 10mV is balanced against a length of 40cm of the potentiometer wire. What is the value of external resistance?
A790ΩB890ΩC990ΩD1090ΩThe potentiometer wire of length 200cm has a resistance of 20Ω. It is connected in series with a resistance 10Ω and an accumulator of emf 6V having negligible internal resistance. A source of 2.4V is balanced against length 1 of the potentiometer wire. Find the length l of the potentiometer wire. Find the length l
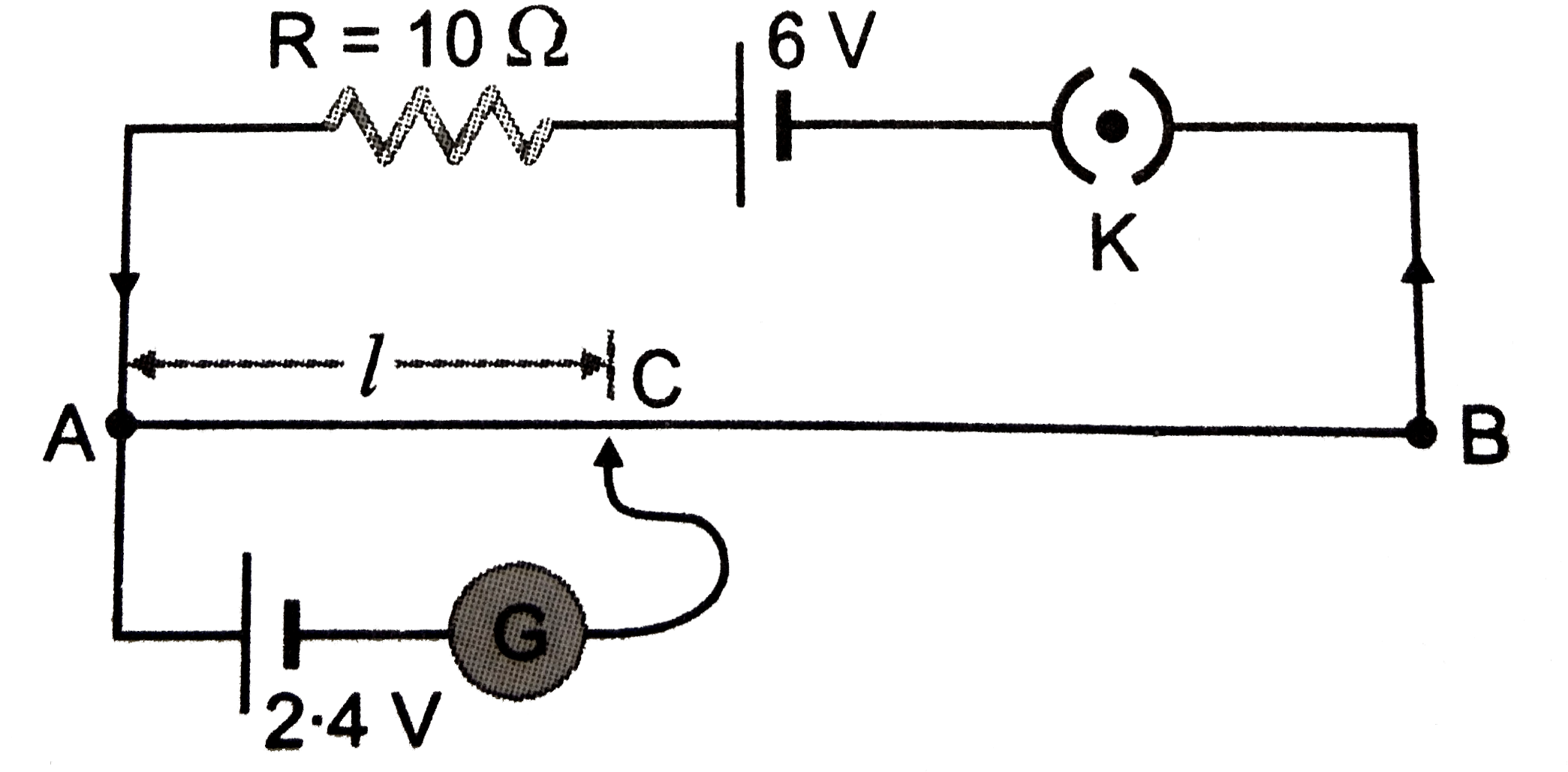 A100cmB120cmC110cmD140cm
A100cmB120cmC110cmD140cm
A potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and negligible resistance. A source of emf 10 mV is balanced against a length of 40cm of the potentiometer wire. What is the value of R?
View Solution
A uniform potentiometer wire AB of length 100 cm has a resistance of 5Ω and it is connected in series with an external resistance R and a cell of emf 6 V and negligible internal resistance. If a source of potential drop 2 V is balanced against a length of 60 cm of the potentiometer wire, the value of resistance R is
View SolutionAB is a potentiometer wire of length 100 cm and its resistance is 10Ω. It is connected in series with a resistance R = 40 Ω and a battery of emf 2 V and negligible internal resistance. If a source of unknown emf E is balanced by 40 cm length of the potentiometer wire, the value of E is
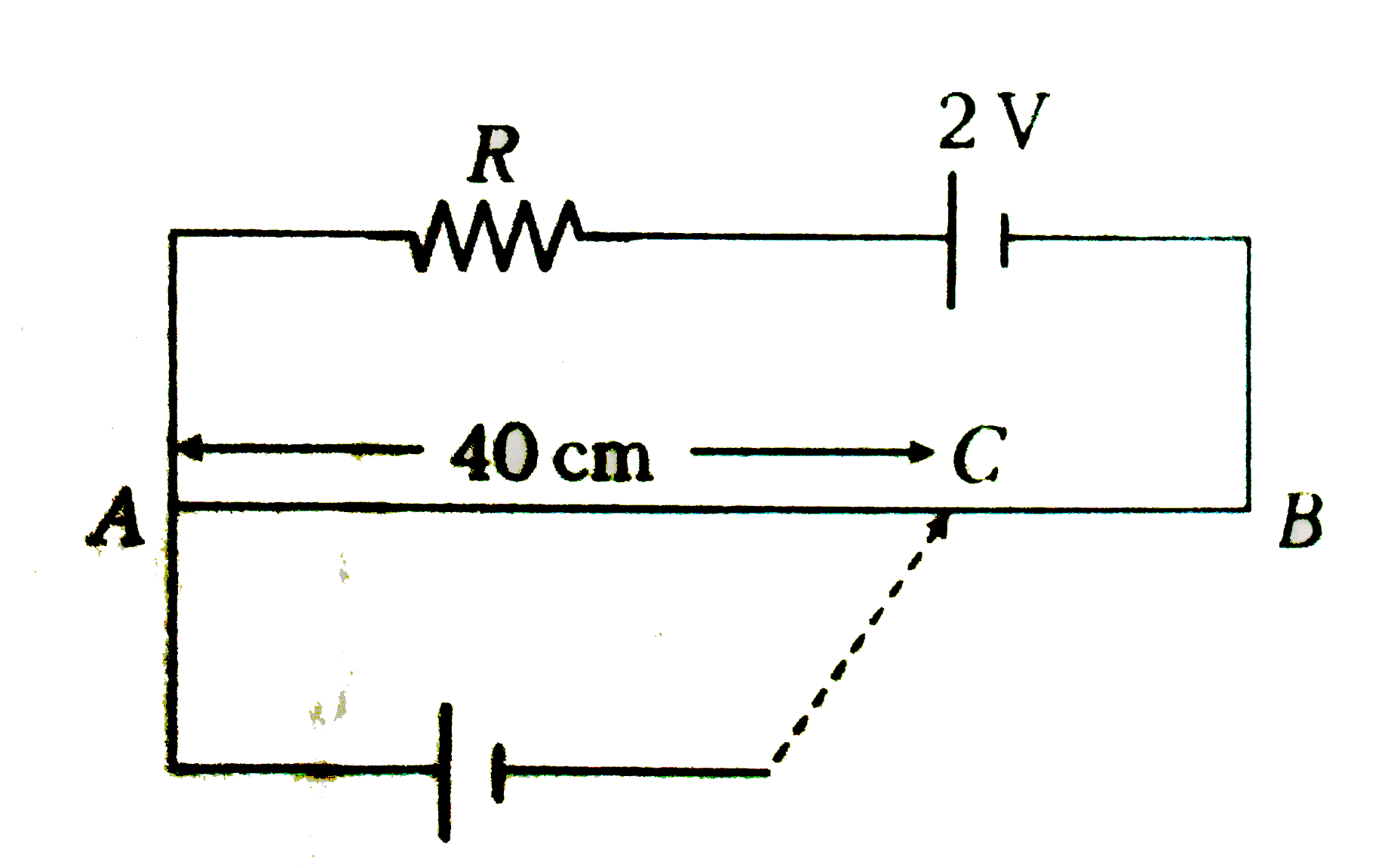
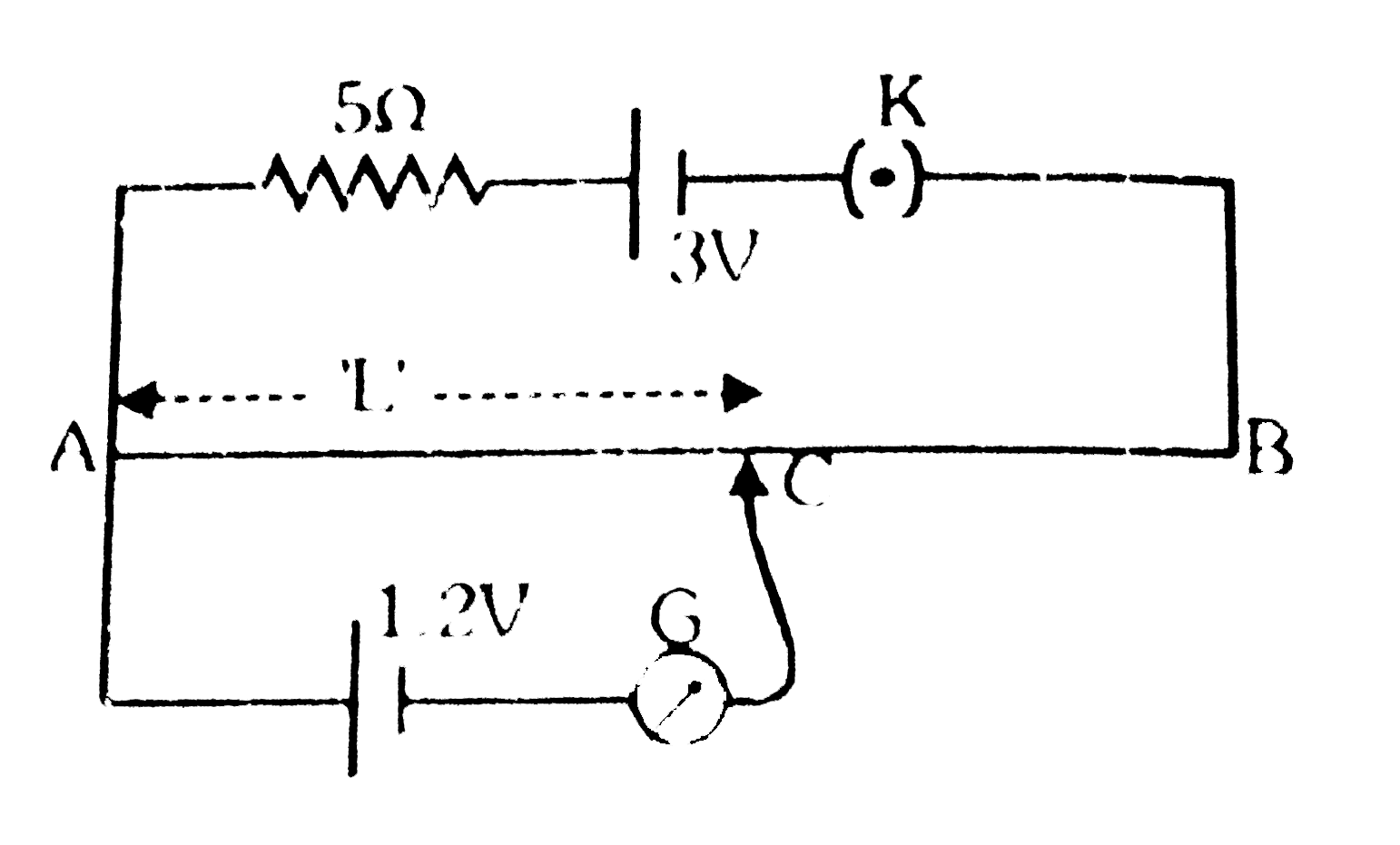
View SolutionThe potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance of 5Ω and an accumulaot or emf 3V having negligible resistance. A source 1.2V is balanced against a length 'L' of the potentionmeter wire. find the value of L.
View SolutionAB is a potentiometer wire of length 100cm and its resistance is 10ohm. It is connected in series with a resistance R=40 ohm and a battery of e.m.f. wV and negigible internal resistance. If a source of unknown e.m.f. E is balanced by 40cm length of the potentiometer wire, the value of E is:

View SolutionA potentiometer wire of length 10 m and resistance 10Ω per meter is connected in serice with a resistance box and a 2 volt battery. If a potential difference of 100 mV is balanced across the whole length of potentiometer wire, then then the resistance introduce introduced in the resistance box will be
View Solution
