In a potentiometer a cell of emf 1.5V gives a balanced point 32cm length of the cell is replaced by another cell then the balance point shifts to 65.0cm the emf of second cell is
3.05V
2.05V
4.05V
6.05V
The correct Answer is:A
To find the EMF of the second cell in the potentiometer setup, we can follow these steps:
1. Understand the Relationship: In a potentiometer, the EMF (E) of a cell is directly proportional to the balancing length (L) on the wire. This can be expressed as:
E1∝L1andE2∝L2
2. Set Up the Ratio: Since the EMFs are proportional to their respective lengths, we can set up a ratio:
E1E2=L1L2
3. Substitute Known Values: We know the following values:
- E1=1.5V (EMF of the first cell)
- L1=32cm (balancing length for the first cell)
- L2=65cm (balancing length for the second cell)
Substituting these values into the ratio gives:
1.5E2=3265
4. Cross-Multiply to Solve for E2: Rearranging the equation to find E2:
1.5×65=E2×32
E2=1.5×6532
5. Calculate E2: Now, perform the calculation:
E2=97.532≈3.04V
6. Conclusion: Therefore, the EMF of the second cell is:
E2≈3.04V
Final Answer:
The EMF of the second cell is 3.04 V.
E1∝L1andE2∝L2
E1E2=L1L2
- E1=1.5V (EMF of the first cell)
- L1=32cm (balancing length for the first cell)
- L2=65cm (balancing length for the second cell)
Substituting these values into the ratio gives:
1.5E2=3265
1.5×65=E2×32
E2=1.5×6532
E2=97.532≈3.04V
E2≈3.04V
The EMF of the second cell is 3.04 V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:HOTS
Explore 8 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:EXEMPLAR PROBLEMS
Explore 6 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:METER BRIDGE
Explore 4 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTPS ENGLISHChapter:COMMUNITCATION SYSTEMSExercise:Assertion And Reason
Explore 30 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
In a potentiometer arrangement, a cell of emf 1.5 V gives a balance point at 27 cm length of wire. If the cell is replaced by another cell and balance point shifts to 54 cm, the emf of the second cell is :
View SolutionIn a potentiometer arrangement a cell of emf 1.5 V gives a balance point at 30 cm length of wire. Now, when the cell is replaced by another celle , the balance point shifts to 50 cm. What is the emf of second cell ?
View SolutionIn a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell ?
View SolutionIn a potentiometer arrangement, a cell of emf 2.25V gives a balance point at 30.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 60.0 cm, then what is the emf of the second cell?
View SolutionIn a potentiometer arrangement , a cell of EMF 2 V gives a balance point at 40 cm length of the wire . If this cell is replaced by another cell and the balance point shifts to 60 cm , then the EMF of the second cell is
View SolutionIn potentiometer experiment, a cell of emf 1.25V gives balancing length of 30 cm. If the cell is replaced by another cell, then balancing length is found to be 40 cm. What is the emf of second cell ?
View SolutionIn a potentiometer arrangement a cell of emf 1.20V given a balance point at 30cm length of the wire. The cell a now replaced by another cell of unknown emf. The ratio of emfs of the two cells is 1.5, calculate the difference in the balancing length of the potentiometer wire in the two cases
View Solutionis made of uniform material and cross-sectional area, and it has uniform resistance per unit length. The potential gradient depends upon the current in the wire.
A potentiometer with a cell of emf 2V and internal resistance 0.4Ω is used across the wire AB. A standard cadmium cell of emf 1.02V gives a balance point at 66cm length of wire. The standard cell is then replaced by a cell of unknows emf e (internal resistance r), and the balance. Point found similarly turns out to be 88cm length of the wire. The length of potentiometer wire AB is 1m.
The reading of the potentiometer, if a 4V battery is used instead of e is
View SolutionFigure shows a potentiometer circuit, a cell of emf E1 is balanced by length l' of the potentiometer wire. If this cell is replaced by another of emf E2, it is found that total length of potentiometer wire has to be increased by 50%, in order to have the same balance length (l'). Then E1/E2 is______.
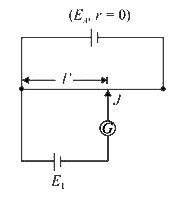
View SolutionFigure shows a potentiometer circuit, a cell of emf E1 is balanced by length l' of the potentiometer wire. If this cell is replaced by another of emf E2, it is found that total length of potentiometer wire has to be increased by 50%, in order to have the same balance length (l'). Then E1/E2 is______.

View Solution

