The volume of vessel A is twice the volume of another vessel B and both of them are filled with the same gas. If the gas in A is at twice the temperature and twice the pressure in comparison to the gas in B, what is the ratio of number of gas molecule in A and B ?
12
21
32
23
The correct Answer is:B
To solve the problem, we will use the Ideal Gas Law, which states that:
PV=nRT
Where:
- P = Pressure
- V = Volume
- n = Number of moles (or number of gas molecules)
- R = Universal gas constant
- T = Temperature
1. Define the Variables:
- Let the volume of vessel B be V.
- Therefore, the volume of vessel A is 2V (since it is twice the volume of B).
- Let the pressure of gas in vessel B be P.
- Therefore, the pressure of gas in vessel A is 2P (since it is twice the pressure of B).
- Let the temperature of gas in vessel B be T.
- Therefore, the temperature of gas in vessel A is 2T (since it is twice the temperature of B).
2. Apply the Ideal Gas Law for Vessel A:
- For vessel A, we can write:
PAVA=nARTA
Substituting the values:
(2P)(2V)=nAR(2T)
Simplifying this:
4PV=2nART
Rearranging gives:
nA=4PV2RT=2PVRT
3. Apply the Ideal Gas Law for Vessel B:
- For vessel B, we can write:
PBVB=nBRTB
Substituting the values:
P(V)=nBR(T)
Rearranging gives:
nB=PVRT
4. Find the Ratio of Number of Gas Molecules:
- Now, we can find the ratio of the number of gas molecules in A and B:
nAnB=2PVRTPVRT=2PVPV=2
5. Conclusion:
- Therefore, the ratio of the number of gas molecules in vessel A to vessel B is:
nAnB=2:1
Final Answer:
The ratio of the number of gas molecules in A and B is 2:1.
---
- P = Pressure
- V = Volume
- n = Number of moles (or number of gas molecules)
- R = Universal gas constant
- T = Temperature
- Let the volume of vessel B be V.
- Therefore, the volume of vessel A is 2V (since it is twice the volume of B).
- Let the pressure of gas in vessel B be P.
- Therefore, the pressure of gas in vessel A is 2P (since it is twice the pressure of B).
- Let the temperature of gas in vessel B be T.
- Therefore, the temperature of gas in vessel A is 2T (since it is twice the temperature of B).
- For vessel A, we can write:
PAVA=nARTA
Substituting the values:
(2P)(2V)=nAR(2T)
Simplifying this:
4PV=2nART
Rearranging gives:
nA=4PV2RT=2PVRT
- For vessel B, we can write:
PBVB=nBRTB
Substituting the values:
P(V)=nBR(T)
Rearranging gives:
nB=PVRT
- Now, we can find the ratio of the number of gas molecules in A and B:
nAnB=2PVRTPVRT=2PVPV=2
- Therefore, the ratio of the number of gas molecules in vessel A to vessel B is:
nAnB=2:1
The ratio of the number of gas molecules in A and B is 2:1.
Topper's Solved these Questions
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Kinetic Theory of An Ideal Gas
18 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - LAW OF EQUIPARTITION OF ENERGY
5 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion And Reason
15 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
15 Videos
Similar Questions
At a given volume and temperature the pressure of a gas
View SolutionFor a given mass of gas the variation of pressure versus temperature is shown in the figure. What is the ratio of volume of the gas at points A and B.
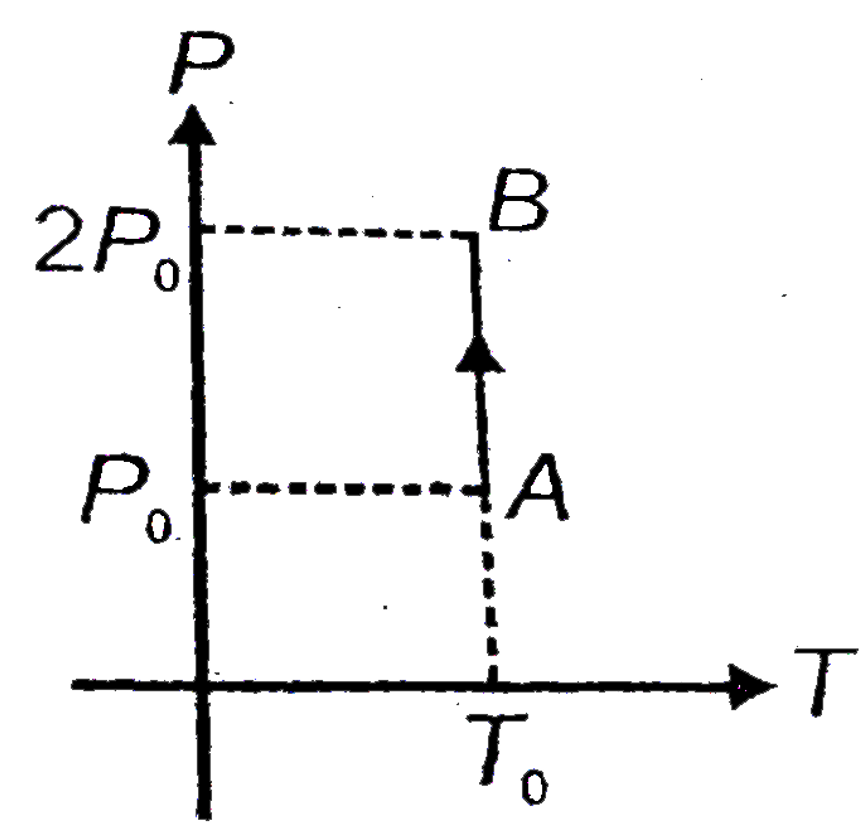 .
.
View SolutionContainers A and B have same gases. Pressure, volume and temperature of A are all twice that of B, then the ratio of number of molecules of A and B are
View SolutionContainers A and B have same gases. Pressure, volume and temperature of A are all twice that of B, then the ratio of number of molecules of A and B are
View SolutionThe pressure P, Volume V and temperature T of a gas in the jar A and the other gas in the jar B at pressure 2P, volume V/4 and temperature 2T, then the ratio of the number of molecules in the jar A and B will be
View SolutionThe volume of a given mass of gas is 20 litre at 300K and 1 atmosphere pressure .At what pressure will the volume of the gas be 1 litre at the same temperature ?
View SolutionTwo balloons are filled one with pure He gas and the other with air respectively. If the pressure and temperature of these balloons are same, then the number of molecules per unit volume is
View SolutionThe density of gas A is twice that of B at the same temperature the molecular weight of gas B is twice that of A. The ratio of pressure of gas A and B will be :
View SolutionThe volumes of gases A, B, C and D are in the ratio, 1:2:2:4 under the same conditions of temperature and pressure.
If the temperature and the pressure of gas A are kept constant, then what will happen to its volume when the number of molecules is doubled?
View SolutionThe density of a gas A is twice that of a gas B at the same temperature. The molecular mass of gas B is thrice that of A. The ratio of the pressure acting on A and B will be
View Solution
