A metal ball B1 (density 3.2g/cc) is dropped in water, while another metal ball B2 (density 6.0g/cc) is dropped in a liquid of density 1.6g/cc. If both the balls have the same diameter and attain the same terminal velocity, the ratio of viscosity of water to that of the liquid is
2
0.5
4
indeterminate due to insufficient data
The correct Answer is:B
To solve the problem, we will use the concept of terminal velocity and the relationship between the viscosity of fluids and the forces acting on the falling balls.
1. Understanding the Problem:
We have two metal balls, B1 and B2, with different densities, dropped in different fluids. We need to find the ratio of the viscosity of water to that of the liquid in which B2 is dropped.
2. Given Data:
- Density of ball B1, σ1=3.2g/cm3
- Density of ball B2, σ2=6.0g/cm3
- Density of water, ρw=1.0g/cm3
- Density of the liquid, ρl=1.6g/cm3
- Both balls have the same diameter and attain the same terminal velocity.
3. Terminal Velocity Formula:
The terminal velocity Vt of a sphere falling through a fluid is given by:
Vt=29r2g(σ−ρ)η
where:
- r = radius of the ball
- g = acceleration due to gravity
- σ = density of the ball
- ρ = density of the fluid
- η = viscosity of the fluid
4. Setting Up the Equations:
For ball B1 (in water):
Vt1=29r2g(σ1−ρw)ηw
For ball B2 (in liquid):
Vt2=29r2g(σ2−ρl)ηl
5. Equating the Terminal Velocities:
Since both balls attain the same terminal velocity:
29r2g(σ1−ρw)ηw=29r2g(σ2−ρl)ηl
We can cancel out common terms:
(σ1−ρw)ηw=(σ2−ρl)ηl
6. Finding the Ratio of Viscosities:
Rearranging the equation gives:
ηwηl=σ1−ρwσ2−ρl
7. Substituting the Values:
- For ball B1:
σ1−ρw=3.2−1.0=2.2g/cm3
- For ball B2:
σ2−ρl=6.0−1.6=4.4g/cm3
Therefore,
ηwηl=2.24.4=12
8. Final Result:
The ratio of the viscosity of water to that of the liquid is:
ηwηl=12
We have two metal balls, B1 and B2, with different densities, dropped in different fluids. We need to find the ratio of the viscosity of water to that of the liquid in which B2 is dropped.
- Density of ball B1, σ1=3.2g/cm3
- Density of ball B2, σ2=6.0g/cm3
- Density of water, ρw=1.0g/cm3
- Density of the liquid, ρl=1.6g/cm3
- Both balls have the same diameter and attain the same terminal velocity.
The terminal velocity Vt of a sphere falling through a fluid is given by:
Vt=29r2g(σ−ρ)η
where:
- r = radius of the ball
- g = acceleration due to gravity
- σ = density of the ball
- ρ = density of the fluid
- η = viscosity of the fluid
For ball B1 (in water):
Vt1=29r2g(σ1−ρw)ηw
For ball B2 (in liquid):
Vt2=29r2g(σ2−ρl)ηl
Since both balls attain the same terminal velocity:
29r2g(σ1−ρw)ηw=29r2g(σ2−ρl)ηl
We can cancel out common terms:
(σ1−ρw)ηw=(σ2−ρl)ηl
Rearranging the equation gives:
ηwηl=σ1−ρwσ2−ρl
- For ball B1:
σ1−ρw=3.2−1.0=2.2g/cm3
- For ball B2:
σ2−ρl=6.0−1.6=4.4g/cm3
Therefore,
ηwηl=2.24.4=12
The ratio of the viscosity of water to that of the liquid is:
ηwηl=12
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Higher Order Thinking Skills
Explore 8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Exemplar Problems
Explore 5 Videos
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:Assertion And Reason
Explore 15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A small metal ball of diameter 4mm and density 10.5g/cm3 in dropped in glycerine of density 1.5g/cm3. The ball attains a terminal velocity of 8cms−1. The coefficient of viscosity of glycerine is
View SolutionA small metal ball of diameter 4mm and density 10.5g/cm3 in dropped in glycerine of density 1.5g/cm3. The ball attains a terminal velocity of 8/cms−1. The coefficient of viscosity of glycerine is
View Solution30 mL of methyl alcohol (density = 0.8 g/cc) is mixed with 70 mL of water (density = 1.0 g/cc) at 25∘C to give a solution of density 0.94 g/cc. Find the mole fraction, molarity and molality.
View SolutionA smooth spherical ball of radius 1cm and density 4×103kg/m3 is dropped gently in a large container containing viscous liquid of density 2×103kg/m3, and η=0.1N−s/m2. The distance moved by the ball in t=0.1sec after it attains terminal velocity is

View SolutionA body of density 2.5g/cm3 is let free in a liquid of density 1.25g/cm3 . The downward acceleration of the of the body while sinking in the liquid is . _______
View SolutionA sphere of radius R is gently dropped into liquid of viscosity η in a vertical uniform tube. It attains a terminal velocity v. Another sphere of radius 2R when dropped into the same liquid, will attain its teriminal velocity.
View Solution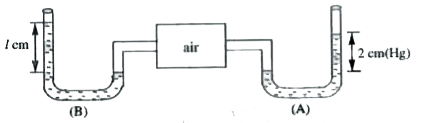
What is l if the liquid in manometre 'B' has a density 1.36 gm/cc.
View SolutionA container filled with a liquid of density 4p as shown in the figure. The velocity efflux through orifice is (ρ is density of water and g = 10 ms−2)
_PHY_E05_013_Q01.png)
View SolutionTwo balls of masses 2 g and 6 g are moving with kinetic energy in the ratio of 3:1. What is the ratio of their linear momentum ?
View SolutionThe coefficient of viscosity of a liquid of σ=1.0CGS units as determined by measuring the terminal velocity of a spherical solid ball of density p=1.5CGS units inside the liquid. If the ball of radius 1.00cm attain terminal velocity 1cm/s, then the viscosity (in CGS units) of the liquid as calculated from the observations of the experimental is: [Take g=10m/s2 ]
View Solution

