A sphere of radius R is gently dropped into liquid of viscosity η in a vertical uniform tube. It attains a terminal velocity v. Another sphere of radius 2R when dropped into the same liquid, will attain its teriminal velocity.
v
2v
4v
9v
The correct Answer is:C
To solve the problem, we need to determine the terminal velocity of a sphere with radius 2R when it is dropped into a viscous liquid, given that a sphere of radius R has a terminal velocity v.
1. Understand the relationship of terminal velocity with radius:
According to Stokes' law, the terminal velocity vt of a sphere falling through a viscous fluid is given by the formula:
vt=2R2(ρ−σ)g9η
where:
- R = radius of the sphere
- ρ = density of the sphere
- σ = density of the fluid
- g = acceleration due to gravity
- η = viscosity of the fluid
2. Identify the terminal velocity for the first sphere:
For the first sphere of radius R, the terminal velocity is:
v=2R2(ρ−σ)g9η
3. Determine the terminal velocity for the second sphere:
For the second sphere of radius 2R, we can substitute 2R into the terminal velocity formula:
vt2=2(2R)2(ρ−σ)g9η
Simplifying this gives:
vt2=2⋅4R2(ρ−σ)g9η=8R2(ρ−σ)g9η
4. Relate the terminal velocities:
Now, we can relate vt2 to v:
vt2=4⋅2R2(ρ−σ)g9η=4v
5. Conclusion:
Thus, the terminal velocity of the second sphere (radius 2R) is:
vt2=4v
Final Answer:
The terminal velocity of the sphere with radius 2R is 4v.
---
According to Stokes' law, the terminal velocity vt of a sphere falling through a viscous fluid is given by the formula:
vt=2R2(ρ−σ)g9η
where:
- R = radius of the sphere
- ρ = density of the sphere
- σ = density of the fluid
- g = acceleration due to gravity
- η = viscosity of the fluid
For the first sphere of radius R, the terminal velocity is:
v=2R2(ρ−σ)g9η
For the second sphere of radius 2R, we can substitute 2R into the terminal velocity formula:
vt2=2(2R)2(ρ−σ)g9η
Simplifying this gives:
vt2=2⋅4R2(ρ−σ)g9η=8R2(ρ−σ)g9η
Now, we can relate vt2 to v:
vt2=4⋅2R2(ρ−σ)g9η=4v
Thus, the terminal velocity of the second sphere (radius 2R) is:
vt2=4v
The terminal velocity of the sphere with radius 2R is 4v.
Similar Questions
The terminal velocity of a sphere of radius R, falling in a viscous fluid, is proportional to
View SolutionA sphere of radius r is dropped in a liquid from its surface. Which of the following graphs is/are correct?

View SolutionA sphere of radius r is dropped in a liquid of viscosity x. Match the Column-I showing some graph with Column-II giving the names of graphs.
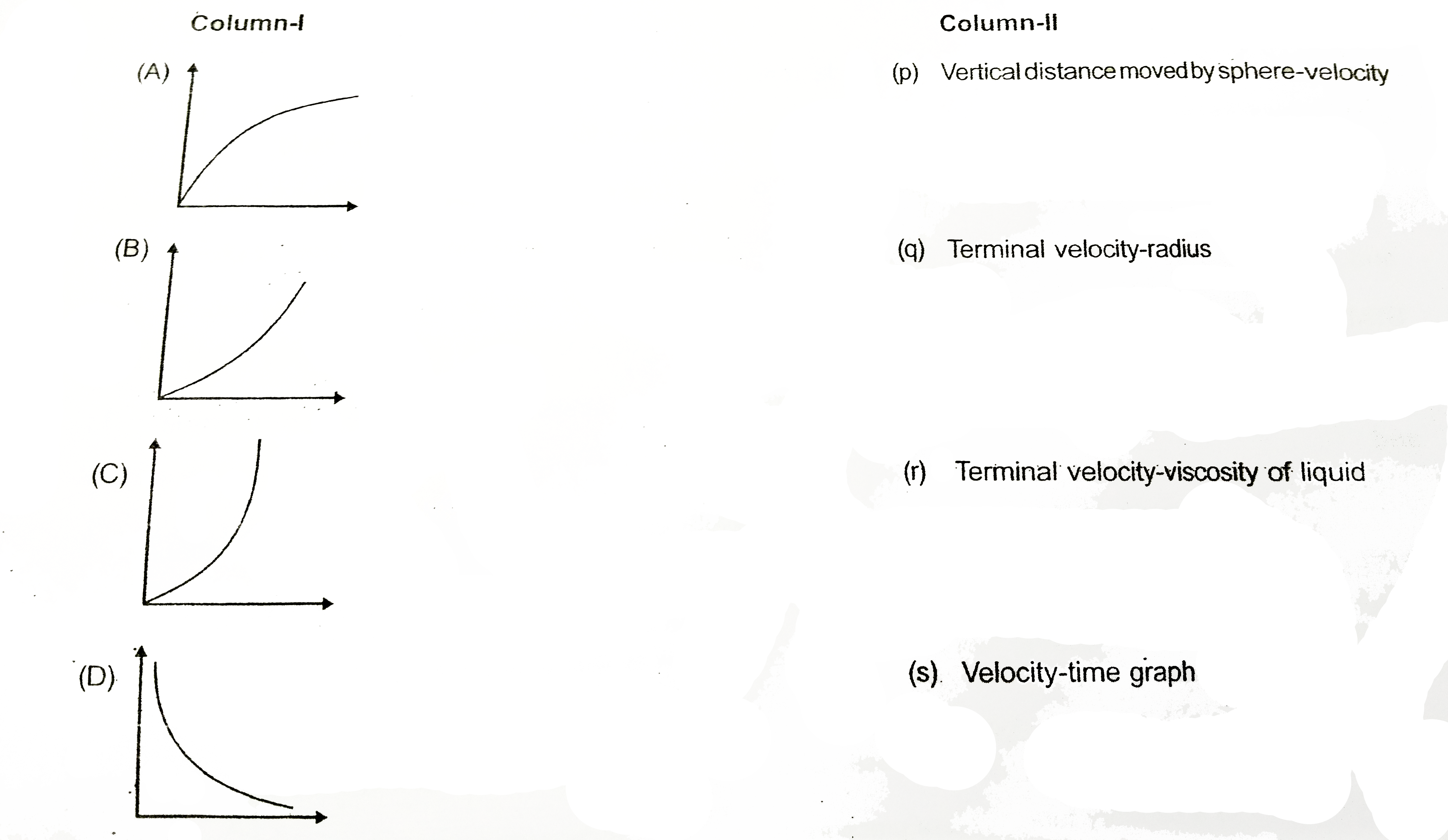
View SolutionThe terminal velocity v of a spherical ball of lead of radius R falling through a viscous liquid varies with R such that
View SolutionChoose the correct option:
When a sphere falling in a viscous fluid attains terminal velocity, then
View SolutionThe ratio of the terminal velocities of two drops of radii R and R/2 is
View SolutionStatement-1 : When two speres of same size but of different densities are dropped in a fluid, sphere of greater density will have greater terminal velocity.
And
Statement-2 : Greater the density and viscosity of the fluid, lesser will be the terminal velocity.
View SolutionA sphere of brass released in a long liquid column attains a terminal speed v0. If the terminal speed is attained by a sphere of marble of the same radius and released in the same liquid is nv0, then the value of n will be (Given: The specific gravities of brass, marble and liquid are 8.5,2.5 and 0.8, respectively)
View SolutionA tiny sphere of mass m and density x is dropped in a jar of glycerine of density y. When the sphere aquires terminal velocity, the magnitude of the viscous force acting on it is :
View SolutionIf the radius of a sphere is 2r , them its volume will be
View Solution

