A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

A
B
C
D
The correct Answer is:A
(a) From Kepler's second law of planetary motion, the linear speed of a planet is maximum when its distance from the sun is least.
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Universal law of Gravitations
14 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - The Gravitational constant
8 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
Similar Questions
Knowledge Check
A planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
Figure shows a planet in an elliptical orbit around the Sun S. Where is the kinetic energy of the planet maximum?

View SolutionA planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
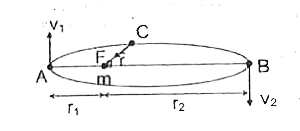
View SolutionA planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:
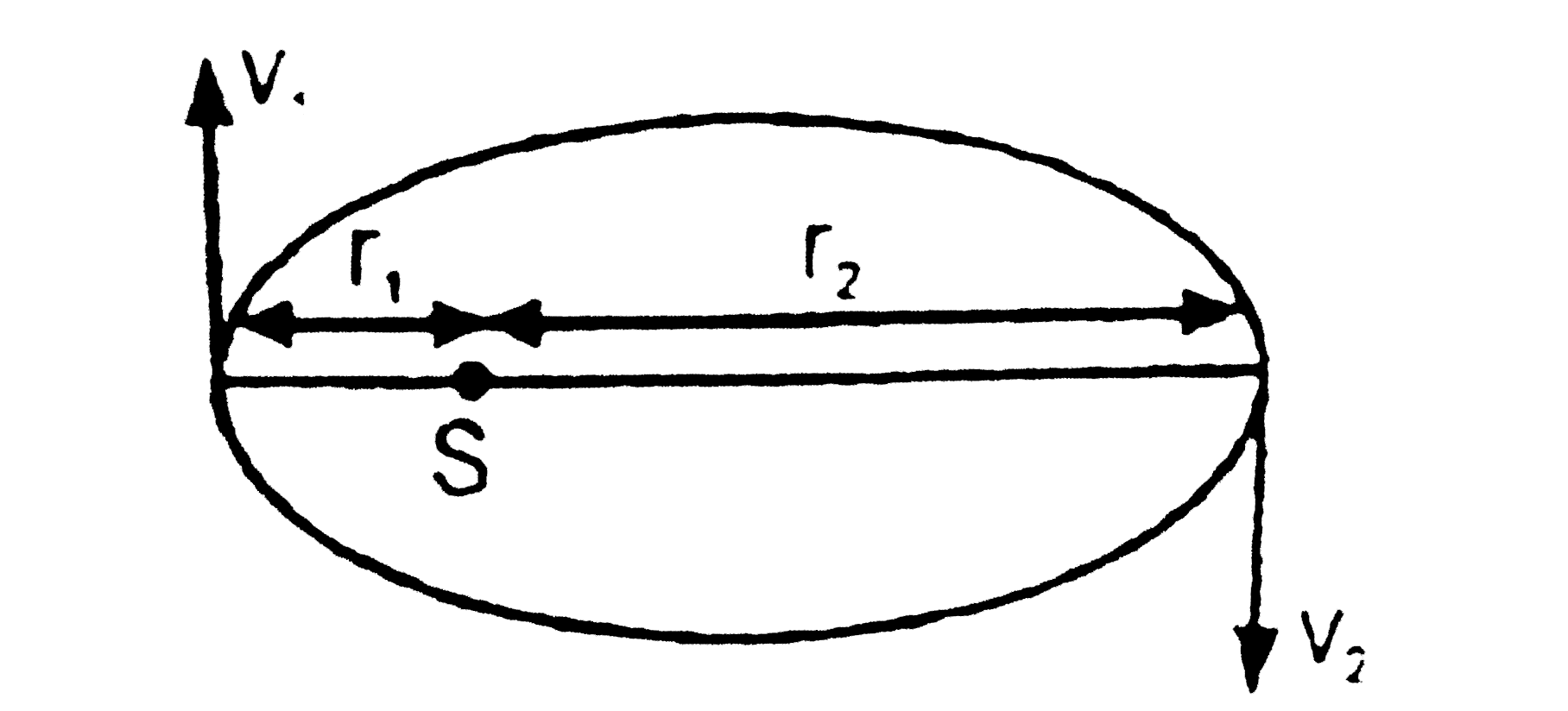
View SolutionIn the figure shown a planet moves in an elliptical orbit around the sun. Compare the speeds, linear and angular momenta at the points A and B.
View SolutionConsider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
View SolutionConsider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
View SolutionA planet travels in an elliptical orbit about a star as shown. At what pair of points is the speed of the planet the same?
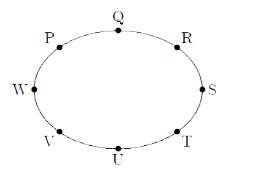
View Solution

