A block of mass m is on an inclined plane of angle θ. The coefficient of friction between the block and the plane is μ and tanθ>μ. The block is held stationary by applying a force P parallel to the plane. The direction of force pointing up the plane is taken to be positive. As P is varied from P1=mg(sinθ−μcosθ) to P2=mg(sinθ+μcosθ), the frictional force f versus P graph will look like
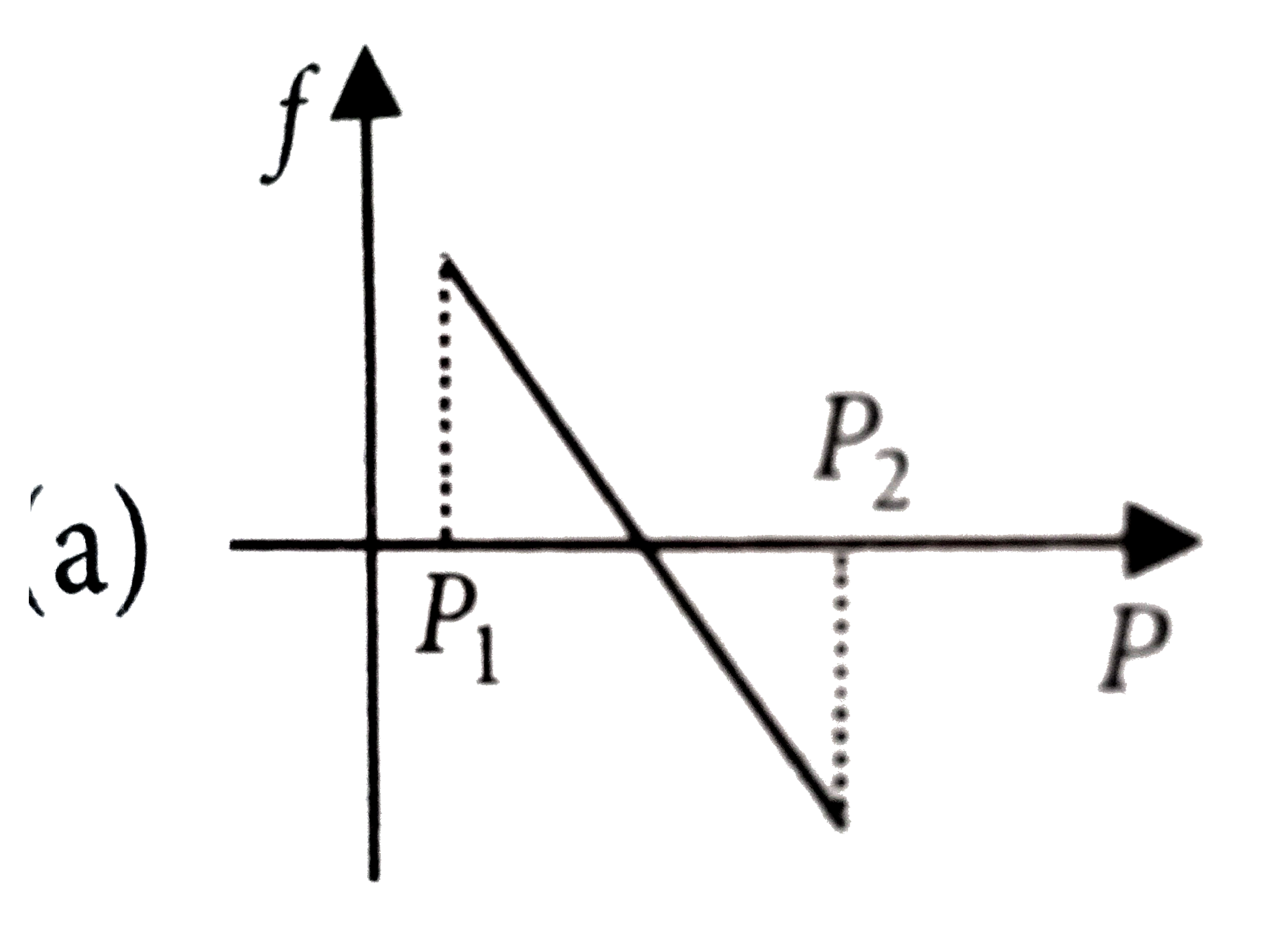
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the block on the inclined plane and how the frictional force varies with the applied force P.
1. Identify the Forces Acting on the Block:
- The weight of the block mg acts downward.
- This weight can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
- The normal force N acts perpendicular to the surface of the incline.
- The frictional force f acts opposite to the direction of motion (or impending motion).
2. Establish the Conditions:
- The block is held stationary by the applied force P parallel to the incline.
- The coefficient of friction is μ, and we know that tanθ>μ.
3. Determine the Frictional Force:
- When the applied force P is less than mgsinθ−μmgcosθ (denoted as P1), the frictional force f will act up the incline to prevent the block from sliding down.
- The equation for equilibrium in this case is:
P+f=mgsinθ
Rearranging gives:
f=mgsinθ−P
4. Frictional Force at Maximum Static Friction:
- When P is increased to P1, the frictional force reaches its maximum static value:
f=μmgcosθ
5. Increasing the Applied Force P:
- As P increases beyond P1, the frictional force will decrease linearly until it reaches zero at P2=mgsinθ+μmgcosθ.
- At this point, the block will start moving up the incline, and the frictional force will act downwards.
6. Graph of Frictional Force f vs. Applied Force P:
- The graph will start from f=mgsinθ−P when P<P1 and will decrease linearly.
- When P exceeds P1, the frictional force will decrease until it reaches zero at P2.
- After P2, the frictional force will act in the opposite direction (down the incline) and can be represented as f=P−mgsinθ.
Final Graph Description:
- The graph of frictional force f versus applied force P will be a linear decreasing line starting from the maximum static friction value at P1 and reaching zero at P2. After P2, the graph will represent a constant downward frictional force as P continues to increase.
- The weight of the block mg acts downward.
- This weight can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
- The normal force N acts perpendicular to the surface of the incline.
- The frictional force f acts opposite to the direction of motion (or impending motion).
- The block is held stationary by the applied force P parallel to the incline.
- The coefficient of friction is μ, and we know that tanθ>μ.
- When the applied force P is less than mgsinθ−μmgcosθ (denoted as P1), the frictional force f will act up the incline to prevent the block from sliding down.
- The equation for equilibrium in this case is:
P+f=mgsinθ
Rearranging gives:
f=mgsinθ−P
- When P is increased to P1, the frictional force reaches its maximum static value:
f=μmgcosθ
- As P increases beyond P1, the frictional force will decrease linearly until it reaches zero at P2=mgsinθ+μmgcosθ.
- At this point, the block will start moving up the incline, and the frictional force will act downwards.
- The graph will start from f=mgsinθ−P when P<P1 and will decrease linearly.
- When P exceeds P1, the frictional force will decrease until it reaches zero at P2.
- After P2, the frictional force will act in the opposite direction (down the incline) and can be represented as f=P−mgsinθ.
- The graph of frictional force f versus applied force P will be a linear decreasing line starting from the maximum static friction value at P1 and reaching zero at P2. After P2, the graph will represent a constant downward frictional force as P continues to increase.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exemplar Problems
9 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion & Reason
15 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
15 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
Similar Questions
A block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View Solution
Knowledge Check
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N
A block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is

View SolutionA block of mass 2 kg slides down an incline plane of inclination 30°. The coefficient of friction between block and plane is 0.5. The contact force between block and plank is :
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View SolutionA block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View Solution
