A mass of 1 kg is suspended by means of a thread. The system is (i) lifted up with an acceleration of 4.9ms2 (ii) lowered with an acceleration of 4.9ms−2. The ratio of tension in the first and second case is
3:1
1:2
1:3
2:1
The correct Answer is:A
To solve the problem, we need to find the tension in the thread when a mass of 1 kg is lifted and lowered with an acceleration of 4.9 m/s². We will denote the tension when the mass is lifted as T1 and when it is lowered as T2.
Step 1: Calculate Tension when the mass is lifted (T1)
When the mass is lifted with an acceleration a=4.9m/s2, the forces acting on the mass are:
- The upward tension T1
- The downward gravitational force mg
The net force acting on the mass can be expressed as:
T1−mg=ma
Rearranging this gives:
T1=mg+ma
Substituting m=1kg, g=9.8m/s2, and a=4.9m/s2:
T1=1×9.8+1×4.9=9.8+4.9=14.7N
Step 2: Calculate Tension when the mass is lowered (T2)
When the mass is lowered with the same acceleration a=4.9m/s2, the forces acting on the mass are:
- The upward tension T2
- The downward gravitational force mg
The net force in this case can be expressed as:
mg−T2=ma
Rearranging this gives:
T2=mg−ma
Substituting m=1kg, g=9.8m/s2, and a=4.9m/s2:
T2=1×9.8−1×4.9=9.8−4.9=4.9N
Step 3: Calculate the ratio of tensions (T1/T2)
Now we can find the ratio of the tensions:
T1T2=14.74.9
Calculating this gives:
T1T2=3
Final Answer
The ratio of tension in the first case (lifted) to the second case (lowered) is:
3:1
When the mass is lifted with an acceleration a=4.9m/s2, the forces acting on the mass are:
- The upward tension T1
- The downward gravitational force mg
T1−mg=ma
Rearranging this gives:
T1=mg+ma
Substituting m=1kg, g=9.8m/s2, and a=4.9m/s2:
T1=1×9.8+1×4.9=9.8+4.9=14.7N
When the mass is lowered with the same acceleration a=4.9m/s2, the forces acting on the mass are:
- The upward tension T2
- The downward gravitational force mg
mg−T2=ma
Rearranging this gives:
T2=mg−ma
Substituting m=1kg, g=9.8m/s2, and a=4.9m/s2:
T2=1×9.8−1×4.9=9.8−4.9=4.9N
Now we can find the ratio of the tensions:
T1T2=14.74.9
Calculating this gives:
T1T2=3
The ratio of tension in the first case (lifted) to the second case (lowered) is:
3:1
Topper's Solved these Questions
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:HOTS
Explore 8 Videos
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:Exemplar Problems
Explore 9 Videos
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:Assertion And Reason
Explore 10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT Exemplar
Explore 5 Videos
Similar Questions
A mass of 1kg is suspended by a thread. It is
1. lifted up with an accleration 4.9m/s2.
2. lowered with an acceleration 4.9 m/s2.
The ratio of the tensions is
View SolutionA boy of mass 40 kg climbs up a rope with an acceleration of 2ms−2 . What is the tension in the rope ?
View SolutionA man of mass 70 kg stands on a weighing machine in a lift, which is moving (a) upwards with a uniform speed of 10ms−1
(b) downwards with a uniform acceleration of 5ms−2
(c) upwards with a uniform acceleration of 5ms−2 What would be the readings on the scale in each case ?
(d) What would be the reading if the lift mechanism failed and it hurtled down freely under gravity ?
View SolutionWhen an empty lift is moving down with an acceleration of g4ms−2 the tension in the cable is 9000N. When the lift is moving up with an acceleration of g3ms−2 the tension in the cable is
View SolutionA man of 60kg mass is in a lift. Find the apparent weight of the man when the lift is moving (a) up with uniform acceleration 4ms−2 (b) down with uniform acceleration of 2ms−2 (g=10ms−2)
View SolutionFind the acceleration of 3kg mass when acceleration of 2kg mass is ms−2 as shwon in fig.
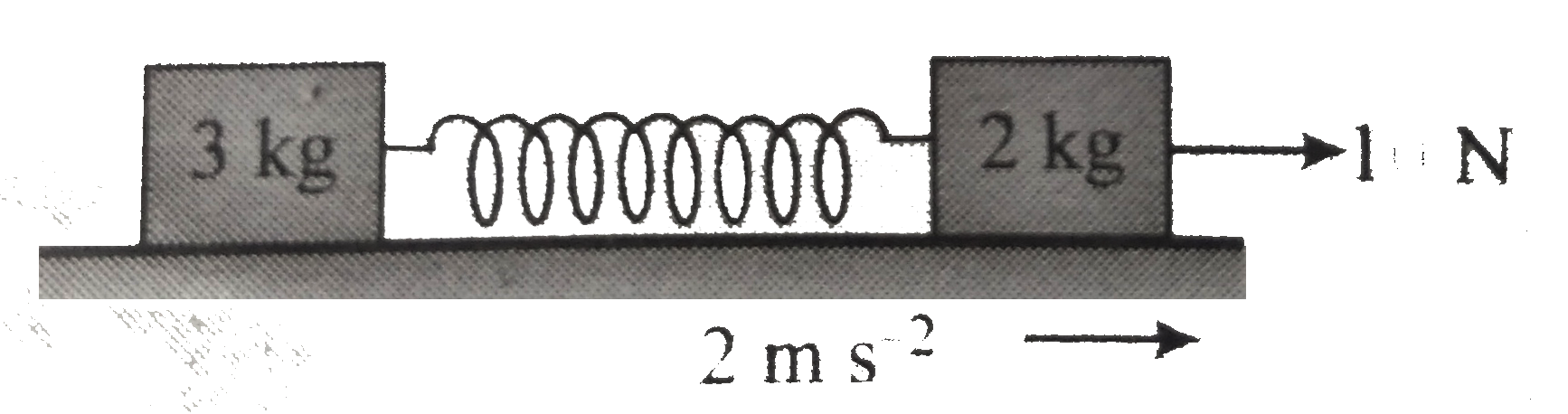
View SolutionA monkey of mass 40 kg climbs on a rope which can withstand a maximum tension of 600 N In which of the following cases will the rope break : The monkey
(a) climbs up with an acceleration of 6ms−2
(b) climbs down with an acceleration of 4ms−2
(c) climbs up with a uniform speed of 5ms−1
(d) falls down the rope nearly freely under gravity ? (Ignore the mass of the rope.)
View SolutionThe mass of a lift if 600kg and it is moving upwards with a uniform acceleration of 2m/s2. Then the tension in the cable of the lift is :
View SolutionA balloon os mass 2 KG is rising up with an acceleration of 4ms2 . The upward force acting on the balloon is (g = 10 ms^-2)
View SolutionA man weighing 60 kg is in a lift moving down with an acceleration of 1.8 ms−2. The force exerted by the floor on him is
View Solution

