In the question number 91, if a force Fis applied to 20 kg block, then the tension in the string is
100N
200N
300N
400N
The correct Answer is:B
To solve the problem of finding the tension in the string when a force F is applied to a 20 kg block, we can follow these steps:
Step 1: Identify the masses and forces
Let:
- m1=10kg (mass of block A)
- m2=20kg (mass of block B)
- F = applied force on block B
- T = tension in the string
- a = acceleration of the system
Step 2: Draw Free Body Diagrams
For block B (20 kg):
- The applied force F acts in the positive direction.
- The tension T acts in the opposite direction.
For block A (10 kg):
- The tension T acts in the positive direction.
- There are no other forces acting on it in the horizontal direction.
Step 3: Write the equations of motion
For block B:
F−T=m2a(1)
For block A:
T=m1a(2)
Step 4: Substitute and solve for acceleration
From equation (2), we can express a in terms of T:
a=Tm1
Substituting this into equation (1):
F−T=m2(Tm1)
Rearranging gives:
F=T+m2Tm1
Factoring out T:
F=T(1+m2m1)
Step 5: Solve for tension T
Now, we can solve for T:
T=F1+m2m1=Fm1+m2m1=F⋅m1m1+m2
Step 6: Substitute known values
Given F=600N, m1=10kg, and m2=20kg:
T=600⋅1010+20=600030=200N
Final Answer:
The tension in the string is T=200N.
---
Let:
- m1=10kg (mass of block A)
- m2=20kg (mass of block B)
- F = applied force on block B
- T = tension in the string
- a = acceleration of the system
For block B (20 kg):
- The applied force F acts in the positive direction.
- The tension T acts in the opposite direction.
- The tension T acts in the positive direction.
- There are no other forces acting on it in the horizontal direction.
For block B:
F−T=m2a(1)
T=m1a(2)
From equation (2), we can express a in terms of T:
a=Tm1
F−T=m2(Tm1)
F=T+m2Tm1
F=T(1+m2m1)
Now, we can solve for T:
T=F1+m2m1=Fm1+m2m1=F⋅m1m1+m2
Given F=600N, m1=10kg, and m2=20kg:
T=600⋅1010+20=600030=200N
The tension in the string is T=200N.
Topper's Solved these Questions
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:HOTS
Explore 8 Videos
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:Exemplar Problems
Explore 9 Videos
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:Assertion And Reason
Explore 10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT Exemplar
Explore 5 Videos
Similar Questions
In the previous question the tension in the string is
View SolutionTwo blocks of masses 6 kg and 4 kg are connected b a rope of mass 2 kg are resting on a frictionless floor as shown in the following figure:

In a constant force of 60N is applied to 6 kg block then the tension in the rope at points A,B and C are respectively given by :
View Solution
Knowledge Check
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400NIn the question number 66, the tension in the string is
A30NB36NC34ND32N
Two identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View SolutionIn the figure shown , two blocks of masses 2 kg and 4kg are connected by a massless string which is just taut (i.e., tension is zero at this moment ). Now two forces 4 N and 15 N are applied on blocks . The tension in the string is (coefficient of static and kinetic friction are same ). [ g = m/s2]
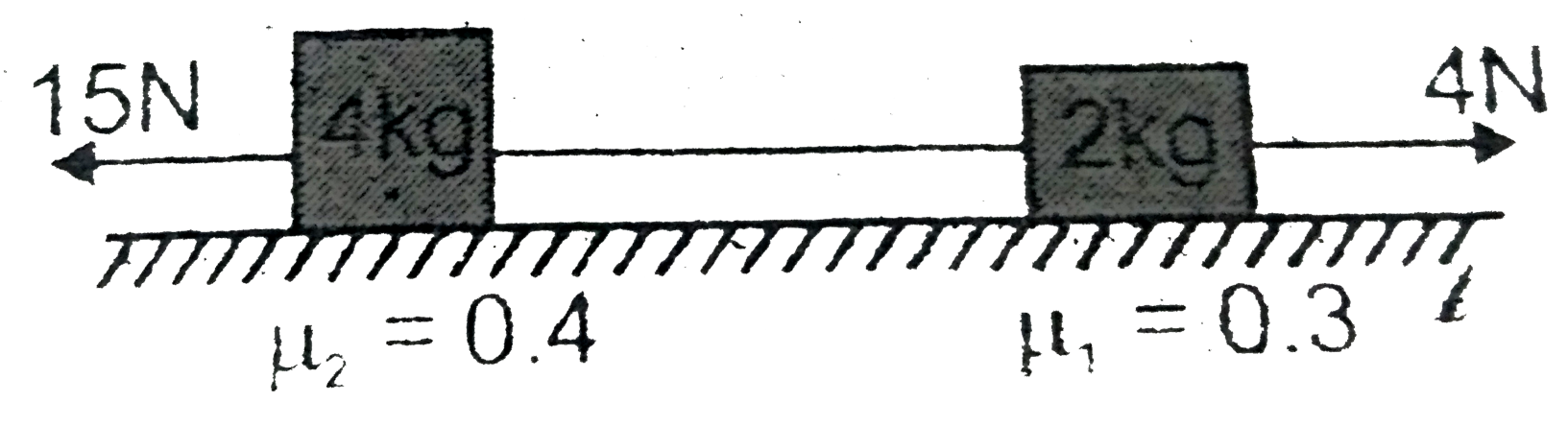
View SolutionTwo blocks of masses 2 kg and 4 kg are connected by a massles string which is just taut. Now two forces 3 N and 14 N are applied on blocks. The tension in the string is
View SolutionA 5 kg block is placed on the top of a 15 kg block as shown in figure . A horizontal force of 60 N is applied to the 15 kg block and the 5kg block is tied to the wall . The coefficient of friction between moving surfaces is 0.2

(a) Draw the free body diagram for each block w.r.t ground and identify the action reaction forces between two blocks .
(b) Determine the tension in the string and magnitude of the acceleration of the 15 kg block .
View Solution
Find out the acceleration of the blocks and tensions in the strings.
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View Solution