When a body slides down from rest along a smooth inclined plane making an angle of 30∘ with the horizontal, it takes time 20s. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it takes time 20p is, where p is some number greater than 1. The coefficient of friction between the body and the rough plane is
μ=(1−1p2)1√3
μ=(1−19p2)
μ=(1−p2)1√3
μ=√1−9p2
The correct Answer is:A
To solve the problem, we need to analyze the motion of a body sliding down both a smooth inclined plane and a rough inclined plane. The steps to find the coefficient of friction between the body and the rough plane are as follows:
Step 1: Analyze the Smooth Inclined Plane
1. Given Data: The angle of inclination θ=30∘ and the time taken t=20 seconds.
2. Acceleration Calculation: For a smooth inclined plane, the only force acting along the incline is the component of gravitational force:
a=gsinθ
where g is the acceleration due to gravity (approximately 10m/s2).
a=10sin(30∘)=10×12=5m/s2
3. Distance Calculation: Using the equation of motion s=ut+12at2:
s=0+12×5×(20)2=12×5×400=1000m
Thus, the length of the incline L=1000m.
Step 2: Analyze the Rough Inclined Plane
1. Given Data: The time taken on the rough incline is t=20p seconds.
2. Net Force Calculation: The net force acting on the body on the rough incline is:
Fnet=mgsinθ−Ffriction=mgsinθ−μmgcosθ
where μ is the coefficient of friction.
Fnet=mg(sinθ−μcosθ)
Dividing by m:
a=g(sinθ−μcosθ)
Substituting θ=30∘:
a=g(12−μ√32)
3. Distance Calculation: Using the same distance s=1000m:
1000=0+12a(20p)2
1000=12(g(12−μ√32))(400p2)
1000=200g(12−μ√32)
Substituting g=10:
1000=2000(12−μ√32)
1=1−√3μ
Rearranging gives:
√3μ=0⟹μ=1−1/p2√3
Final Step: Coefficient of Friction
The coefficient of friction μ is given by:
μ=1−1p2√3
1. Given Data: The angle of inclination θ=30∘ and the time taken t=20 seconds.
2. Acceleration Calculation: For a smooth inclined plane, the only force acting along the incline is the component of gravitational force:
a=gsinθ
where g is the acceleration due to gravity (approximately 10m/s2).
a=10sin(30∘)=10×12=5m/s2
s=0+12×5×(20)2=12×5×400=1000m
Thus, the length of the incline L=1000m.
1. Given Data: The time taken on the rough incline is t=20p seconds.
2. Net Force Calculation: The net force acting on the body on the rough incline is:
Fnet=mgsinθ−Ffriction=mgsinθ−μmgcosθ
where μ is the coefficient of friction.
Fnet=mg(sinθ−μcosθ)
Dividing by m:
a=g(sinθ−μcosθ)
Substituting θ=30∘:
a=g(12−μ√32)
1000=0+12a(20p)2
1000=12(g(12−μ√32))(400p2)
1000=200g(12−μ√32)
Substituting g=10:
1000=2000(12−μ√32)
1=1−√3μ
Rearranging gives:
√3μ=0⟹μ=1−1/p2√3
The coefficient of friction μ is given by:
μ=1−1p2√3
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - HOTS
8 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exemplar Problems
9 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
Similar Questions
When body slides down from rest along smooth inclined plane making angle of 45∘ with the horizontal, it takes time T When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance it is seen to take time pT, where p is some number greater that 1. Calculate late the coefficient of friction beween the body and the rough plane.
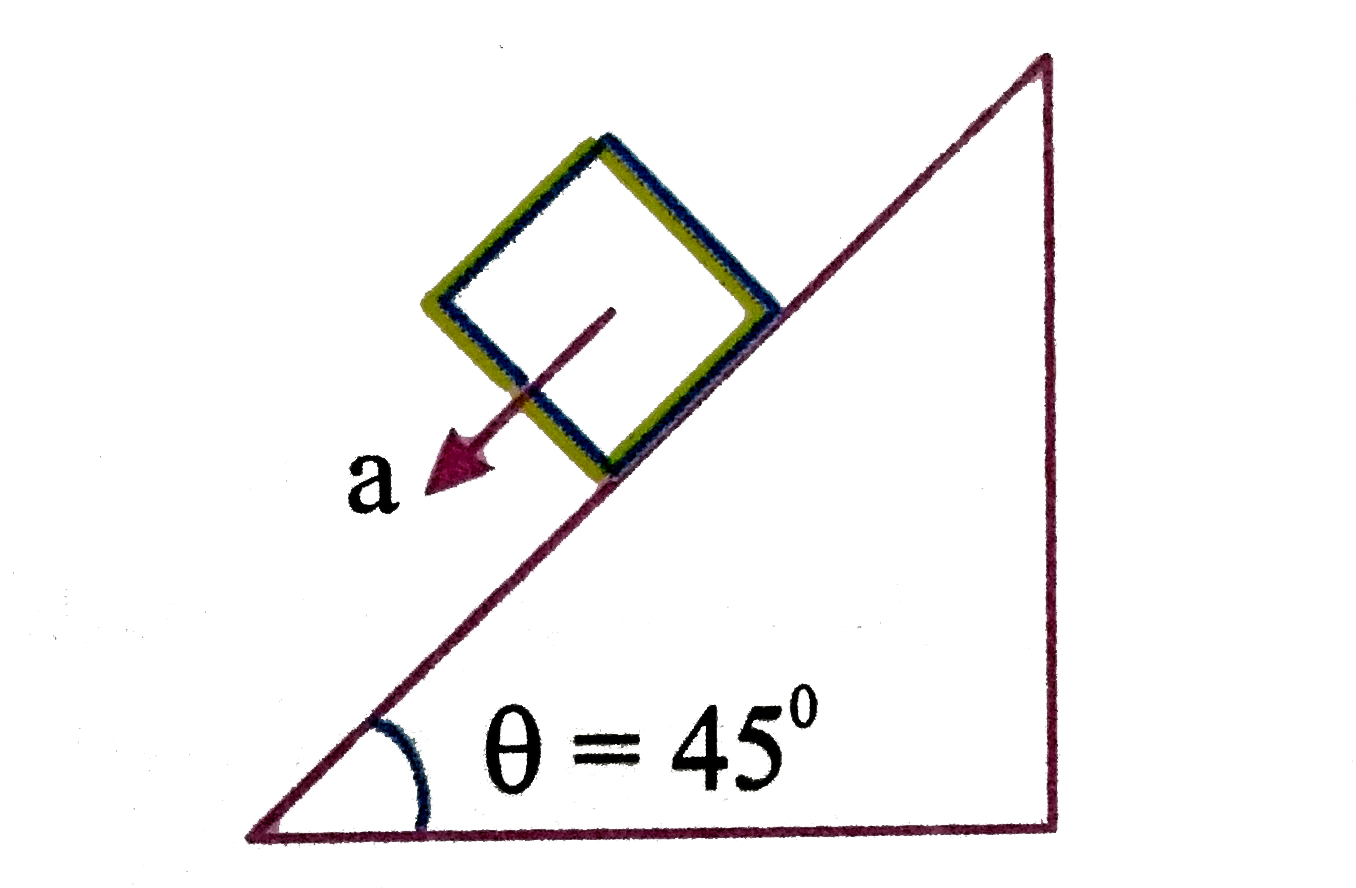 .
.
View SolutionStarting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View Solution
Knowledge Check
When body slides down from rest along smooth inclined plane making angle of 45∘ with the horizontal, it takes time T When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance it is seen to take time pT, where p is some number greater that 1. Calculate late the coefficient of friction beween the body and the rough plane.
 .A1/PBμ=(1−1/p2)C1/p2D2-p
.A1/PBμ=(1−1/p2)C1/p2D2-pStarting from rest, a body slides down a 45∘ inclined plane in twice the time it itakes to slide the same distance in the absence of friction.
They the coefficient of friction between the body and the inclined plane isA1/4B2/3C3/4D√3/2
A body is pushed up on a rough inclined plane making an angle 30∘ to the horizontal. If its time of ascent on the plane is half the time of its descent, find coefficient of friction between the body and the incined plane.
View SolutionIn the case of a body sliding down a rough inclined plane show that μs=tanθ
View SolutionA block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. If μS=0.6 , what is the frictional force on the block ?
View SolutionA body takes ''n'' times as much time to slide down a rough inclined plane as it takes to slide down an identical but smooth inclined plane. If the angle of inclination of the inclined plane is ''θ''. What is the coefficient of friction between the body and the rough plane ?
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination θ . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by -
View SolutionA body weighs 64 N on the surface of the Earth. What is the gravitational force on it (in N) due to the Earth at a height equal to one-third of the radius of the Earth?
View Solution
