A ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
2mu
mu
zero
−2mu
The correct Answer is:D
To solve the problem of finding the impulse imparted to a ball by a rigid wall when it strikes and rebounds, we can follow these steps:
Step 1: Understand the Initial and Final Momentum
- The ball has a mass m and strikes the wall with a speed u.
- The initial momentum (pi) of the ball before it strikes the wall is given by:
pi=m⋅u
Step 2: Determine the Final Momentum
- After striking the wall, the ball rebounds with the same speed u but in the opposite direction. Therefore, the final momentum (pf) is:
pf=m⋅(−u)=−m⋅u
Step 3: Calculate the Change in Momentum
- The impulse (J) imparted to the ball by the wall is equal to the change in momentum. This can be expressed as:
J=pf−pi
- Substituting the values we found for initial and final momentum:
J=(−m⋅u)−(m⋅u)
Step 4: Simplify the Expression
- Simplifying the expression gives:
J=−m⋅u−m⋅u=−2m⋅u
Step 5: Conclusion
- The impulse imparted to the ball by the wall is:
J=−2m⋅u
- The negative sign indicates that the direction of the impulse is opposite to the direction of the initial momentum.
Final Answer
The impulse imparted to the ball by the wall is −2mu.
---
- The ball has a mass m and strikes the wall with a speed u.
- The initial momentum (pi) of the ball before it strikes the wall is given by:
pi=m⋅u
- After striking the wall, the ball rebounds with the same speed u but in the opposite direction. Therefore, the final momentum (pf) is:
pf=m⋅(−u)=−m⋅u
- The impulse (J) imparted to the ball by the wall is equal to the change in momentum. This can be expressed as:
J=pf−pi
- Substituting the values we found for initial and final momentum:
J=(−m⋅u)−(m⋅u)
- Simplifying the expression gives:
J=−m⋅u−m⋅u=−2m⋅u
- The impulse imparted to the ball by the wall is:
J=−2m⋅u
- The negative sign indicates that the direction of the impulse is opposite to the direction of the initial momentum.
The impulse imparted to the ball by the wall is −2mu.
Topper's Solved these Questions
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:HOTS
Explore 8 Videos
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:Exemplar Problems
Explore 9 Videos
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:Assertion And Reason
Explore 10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT Exemplar
Explore 5 Videos
Similar Questions
A ball of mass m strikes a rigid wall with speed v and gets reflected without any loss of speed, as shown in the figure.
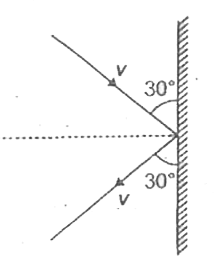
(a) What is the magnitude of the impulse imparted to the ball by the wall?
(b) What is the direction of the force on the wall due to the ball?
View SolutionTwo billiard balls each of mass 0.05 kg moving in opposite directions with speed 6ms−1 collide and rebound with the same speed. What is the impulse imparted to each ball due to the other ?
View Solution
Knowledge Check
A ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzeroTwo billiard ball A and B each of mass 50g and moving in opposite direction with speed of 5ms−1 each, collide and rebound with the same speed. The impulse imparted to each ball is
A0.25kgms−1B0.5kgms−1C0.8kgms−1D0.125kgms−1
A body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View Solution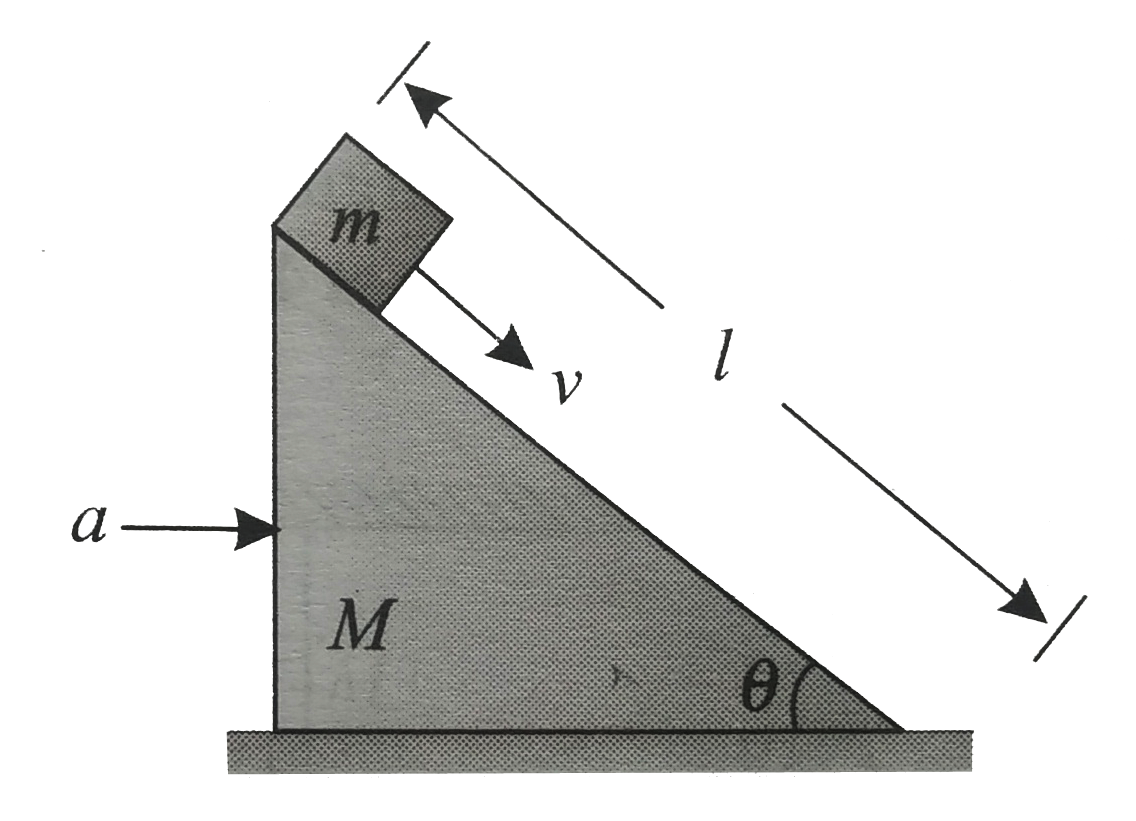
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 600 gm strikes a wall with a velocity of 5ms−1 at an angle 30∘ with the wall and rebounds with the same speed at the same angle with the wall. The change in momentum of the ball is, (in kg ms−1)
View SolutionSTATEMENT - 1 : A ball of mass m is moving towards a batsman at a speed v. The batsman strikes the ball and deflects it by an angle θ without changing its speed. The impulse imparted to the ball is zero.
because
STATEMENT - 2 : Impulse = change in momentum.
View Solution

