Find the relative error in Z, if Z=A4B1/3/CD3/2.
ΔZZ=4ΔAA+13ΔBB+ΔCC+32ΔDD
ΔZZ=4ΔAA+13ΔBB−ΔCC−32ΔDD
ΔZZ=4ΔAA+13ΔBB+ΔCC−32ΔDD
ΔZZ=4ΔAA+13ΔBB−ΔCC+32ΔDD
The correct Answer is:A
To find the relative error in the quantity Z, given by the equation:
Z=A4B1/3CD3/2
we will follow these steps:
Step 1: Identify the formula for relative error
The relative error in a quantity can be expressed as:
ΔZZ
where ΔZ is the absolute error in Z.
Step 2: Apply the error propagation formula
For a function of multiple variables, the relative error can be calculated using the formula:
ΔZZ=∑(power of each variable×Δvariablevariable)
Step 3: Differentiate the components of Z
In our case, we have:
- A raised to the power of 4
- B raised to the power of 13
- C raised to the power of 1 (in the denominator)
- D raised to the power of 32 (in the denominator)
Step 4: Write the contributions to the relative error
Now we can express the relative error in Z as follows:
ΔZZ=4ΔAA+13ΔBB+1ΔCC+32ΔDD
Step 5: Combine the terms
Putting it all together, we have:
ΔZZ=4ΔAA+13ΔBB+ΔCC+32ΔDD
This expression gives us the relative error in Z.
Final Answer
Thus, the relative error in Z is:
ΔZZ=4ΔAA+13ΔBB+ΔCC+32ΔDD
---
The relative error in a quantity can be expressed as:
For a function of multiple variables, the relative error can be calculated using the formula:
In our case, we have:
- B raised to the power of 13
- C raised to the power of 1 (in the denominator)
- D raised to the power of 32 (in the denominator)
Now we can express the relative error in Z as follows:
Putting it all together, we have:
Thus, the relative error in Z is:
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Higher Order Thinking Skills
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Exemplar Problems
12 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assertion And Reason
15 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
statement-1 Let z1,z2 and z3 be htree complex numbers, such that |3z1+1|=|3z2+1|=|3z3+1| and 1+z1+z2+z3=0, then z1,z2,z3 will represent vertices of an equilateral triangle on the complex plane.
statement-2z1,z2,z3 represent vertices of an triangle, if
z21+z22+z23+z1z2+z2z3+z3z1=0
View SolutionLet A(z1),B(z2),C(z3) be the vertices of an equilateral triangle ABC in the Argand plane, then the number z2−z32z1−z2−z3, is
View SolutionThere are three elements A, B and C. their atomic number are Z1,Z2 and Z3 respectively. If Z1−Z2=2andZ1+Z22=Z3−2 and the electronic configuration of element A is [Ar]3d64s2, then correct order of magnetic momentum is/are:
View SolutionThere are three elements A, B and C. their atomic number are Z1,Z2 and Z3 respectively. If Z1−Z2=2andZ1+Z22=Z3−2 and the electronic configuration of element A is [Ar]3d64s2, then correct order of magnetic momentum is/are:
View SolutionLet z1,z2andz3 be three complex numbers such that z1+z2+z3=z1z2+z2z3+z1z3=z1z2z3=1. Then the area of triangle formed by points A(z1),B(z2)andC(z3) in complex plane is _______.
View SolutionIf |z1|=|z2|=|z3|=1 and z1+z2+z3=0 then the area of the triangle whose vertices are z1,z2,z3 is 3√3/4 b. √3/4 c. 1 d. 2
View SolutionFind the equation of line through (−4,1,3) & parallel to the plane x+y+z=3 while the line intersects another line whose eqution is x+y−z=x+2y−3z+5 (a) x+4−3=y−1−2=z−31 (b) x+41=y−12=z−3−3 (c) x+4−3=y−12=z−31
View SolutionFind the minimum value of ∣z−1 if ||z−3|−|z+1∣∣=2.
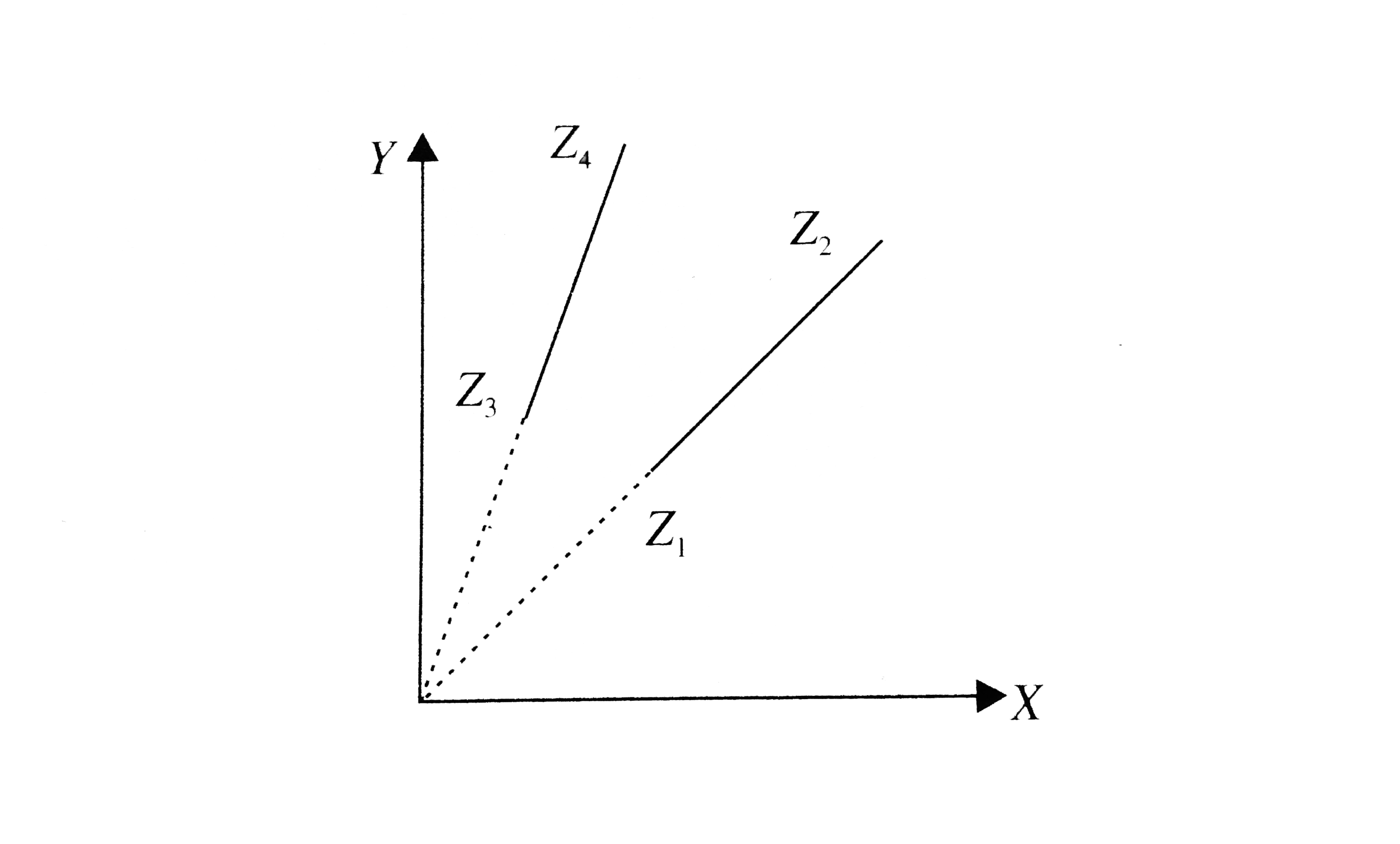
View SolutionIn the diagram as shown, find parameters representing x and y axes and also parameter Z, if Z1=Z2,Z3=Z4 and Z2>Z3:
View SolutionLet A(z1),B(z2),C(z3 and D(z4) be the vertices of a trepezium in an Argand plane such that AB∣∣CD Let |z1−z2|=4,|z3,z4|=10 and the diagonals AC and BD intersects at P. It is given that Arg(z4−z2z3−z1)=π2 and Arg(z3−z2z4−z1)=π4
Which of the following option(s) is/are correct?
View Solution

