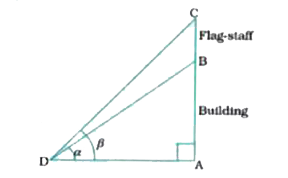
A building stands on a horizontal plane and is surmounted by a vertical flag-stagg of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are αandβ respectively. Prove that the height of the building is htanαtanβ−tanα
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:htanαtanβ−tanα
Step by step video, text & image solution for A building stands on a horizontal plane and is surmounted by a vertical flag-stagg of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are alpha and beta respectively. Prove that the height of the building is (h tan alpha)/(tan beta-tan alpha) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOME AAPLICATIONS OF TRIGONOMETRYBook:KUMAR PRAKASHANChapter:SOME AAPLICATIONS OF TRIGONOMETRYExercise:Exercise9.1
Explore 16 Videos
- SOME AAPLICATIONS OF TRIGONOMETRYBook:KUMAR PRAKASHANChapter:SOME AAPLICATIONS OF TRIGONOMETRYExercise:Test Your Skills
Explore 5 Videos
- SOME AAPLICATIONS OF TRIGONOMETRYBook:KUMAR PRAKASHANChapter:SOME AAPLICATIONS OF TRIGONOMETRYExercise:Objective Questions
Explore 24 Videos
- REAL NUMBERS Book:KUMAR PRAKASHANChapter:REAL NUMBERS Exercise:TEST YOUR SKILLS
Explore 26 Videos
- STATISTICSBook:KUMAR PRAKASHANChapter:STATISTICSExercise:Objective Questions (True or false)
Explore 5 Videos
Similar Questions
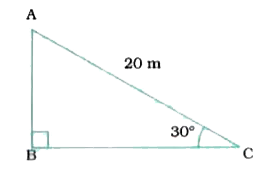
A circus artist is climbing a 20m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30∘ (see the given figure)
View SolutionThe angle of elevation of the top of a tower 30m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top the second tower from the foot of the first tower is 30∘. Find the distance between the two towers and also find the height of the other tower.
View SolutionA kite is flying at a height of 75m from the level ground, attached to a taut string inclined at 60∘ to the horizontal. Then, the length of the string is …………m
View SolutionShow that the square of any positive integer is of the form 4m or 4m + 1 for some integer m.
View SolutionFor any frequency distribution, mean is always greater than mode.
View SolutionA vertical tower Stands on a horizontal plane and is surmounted by a vertical flag staff of height h.At a point on the plane,the angles of Elevation of the bottom and the top of the flag staff are alpha and beta respectively Prove that the height of the tower is (h tan alpha)/(tan beta-tan alpha)
View SolutionA vertical tower stand on a horizontal plane and is surmounted by a vertical flag-staff of height 5 metres. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300and600. Find the height of the tower.
View SolutionA vertical tower sands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β .Prove that the height of the tower htanαtanβ−tanα
View SolutionA vertical tower stands on a horizontal plane and is surmounted by a flag-staff of height 7m. From a point on the plane, the angle of elevation of the bottom of the flag-staff is 30o and that of the top of the flag-staff is 45o . Find the height of the tower.
View Solutionएक उर्ध्वाधर मीनार एक श्रीटीज़ समतल पर खड़ी है और उसके उपर h उचाई का उर्ध्वाधर ध्वजदंड लगा है । समतल पर एक बिन्दू पर ध्वजदंड के तल का उन्नयन कोड α है और ध्वजदंड के शीर्ष भाग का β है। मीनार की उचाई बताइये ?
View Solutionएक उदग्र मीनार क्षैतिज तल पर खड़ा है और इसके शिखर पर h ऊँचाई का एक ध्वजदंड है। क्षैतिज तल पर के बिंदु पर ध्वजदंड के पाद एवं शिखर के उन्नयन कोण क्रमशः α औरβ है। सिद्ध कीजिए कि मीनार कि ऊँचाई htanαtanβ−tanα हैं।
View SolutionA flag staff of length 'd' stands on tower of height h. IF at a point on the ground the angle of elevation of the tower and top of the flag staff be α,β then h=
View SolutionA vertical tower Stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of Elevation of the bottom and the top of the flag staff are αandβ respectively Prove that the height of the tower is htanαtanβ−tanα
View SolutionA vertical tower stand on a horizontal plane and is surmounted by a vertical flag-staff of height 5 metres. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
View SolutionA vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of Elevation of the bottom and the top of the flag staff are αandβ respectively. Prove that the height of the tower is htanαtanβ−tanα
View Solution

