If the angle of elevation of a cloud from a point h metres above the surface of a lake is α and the angle of depression of its reflexion in the lake is β, prove that the height of the cloud is h(tanβ+tanα)tanβ−tanα metres.Solution in Gujrati
The correct Answer is:=h(tanβ+tanα)tanβ−tanα
Step by step video, text & image solution for If the angle of elevation of a cloud from a point h metres above the surface of a lake is alpha and the angle of depression of its reflexion in the lake is beta, prove that the height of the cloud is (h (tan beta + tan alpha))/(tan beta - tan alpha) metres. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOME AAPLICATIONS OF TRIGONOMETRYBOOK - KUMAR PRAKASHANCHAPTER - SOME AAPLICATIONS OF TRIGONOMETRYEXERCISE - Exercise9.1
16 Videos
- SOME AAPLICATIONS OF TRIGONOMETRYBOOK - KUMAR PRAKASHANCHAPTER - SOME AAPLICATIONS OF TRIGONOMETRYEXERCISE - Test Your Skills
5 Videos
- SOME AAPLICATIONS OF TRIGONOMETRYBOOK - KUMAR PRAKASHANCHAPTER - SOME AAPLICATIONS OF TRIGONOMETRYEXERCISE - Objective Questions
24 Videos
- REAL NUMBERS BOOK - KUMAR PRAKASHANCHAPTER - REAL NUMBERS EXERCISE - TEST YOUR SKILLS
26 Videos
- STATISTICSBOOK - KUMAR PRAKASHANCHAPTER - STATISTICSEXERCISE - Objective Questions (True or false)
5 Videos
Similar Questions
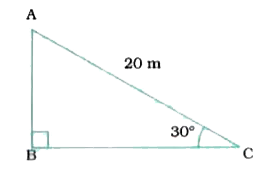
A circus artist is climbing a 20m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30∘ (see the given figure)
View SolutionThe angle of elevation of the top of a tower 30m high from the foot of another tower in the same plane is 60∘ and the angle of elevation of the top the second tower from the foot of the first tower is 30∘. Find the distance between the two towers and also find the height of the other tower.
View SolutionA kite is flying at a height of 75m from the level ground, attached to a taut string inclined at 60∘ to the horizontal. Then, the length of the string is …………m
View SolutionShow that the square of any positive integer is of the form 4m or 4m + 1 for some integer m.
View SolutionFor any frequency distribution, mean is always greater than mode.
View SolutionIf the angle of elevation of the cloud from a point hm above a lake is A and the angle of depression of its reflection in the lake is B prove that the height of the cloud is h(tan B+tan A)tan B-tan A
View SolutionIf the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the take is β , prove that the height of the cloud is h(tanβ+tanα)tanβ−tanα
View SolutionIf the angle of elevation of a cloud from a point h metres above lake is α and the angle of depression of its reflection in the lake be β, prove that the distance of the cloud from the point of observation is 2hsecαtanβ−tanα
View Solutionएक झील से h मीटर ऊँचाई पर बादलों का उन्नयन कोण α है तथा झील में उसकी परछाई का अवनमन कोण β है। सिद्ध कीजिए की बादलों की ऊंचाई h(tanβ+tanα)tanβ−tanα है।
View Solutionबादलों से एक झील पर स्थित बिंदु पर उन्नयन कोण α है तथा इसकी झील की परछाई का अवनमन कोण β है सिद्ध कीजिए| की बादलों से निरिक्षण बिंदु के बीच की दुरी 2hsecαtanβ−tanα है|
View SolutionFrom a point a metres above a lake the angle of elevation of a cloud is α and the angle of depression of its reflection is β. Prove tha the height of the cloud is
asin(α+β)sin(β−α) metres.
View Solutionझील की सतह से h मीटर ऊँचे एक बिन्दु से एक बादल का उन्नयन कोण αतथा झील में बादल के प्रतिबिम्ब का अवनमन कोण β है | सिध्द करो कि प्रेक्षण बिन्दु से बादल की दूरी 2hsecαtanβ−tanαहै |
View Solutionएक झील के तल से 'h ' मीटर ऊंचाई पर स्थित किसी बिंदु से बादल का उनयन कोण α और झील में उसके प्रतिबिम्ब का अवनमन कोण β है सिद्ध कीजिएः की बादल से उस बिंदु की दुरी 2hsecαtanβ−tanα है
View SolutionThe angle of elevation of a cloud from a point h metres above the surface of a lake is α and the angle of depression of its reflection in the lake is β then the height is :
View SolutionIf the angle of elevation of a cloud from a point h metres above lake is α and the angle of depression of its reflection in the lake be β, prove that the distance of the cloud from the point of observation is 2hsecαtanβ−tanα
View Solution
