In △ABC, AD, BE, CF are the medians. Prove that, 4(AD2+BE2+CF2)=3(AB2+BC2+AC2). Solution in Gujrati
The correct Answer is:4(AD2+BE2+CF2)=3(AB2+BC2+AC2)
Step by step video, text & image solution for In triangleABC, AD, BE, CF are the medians. Prove that, 4(AD^(2)+BE^(2)+CF^(2))= 3(AB^(2)+BC^(2)+AC^(2)). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:KUMAR PRAKASHANChapter:TRIANGLESExercise:EXERCISE 6.1
Explore 7 Videos
- TRIANGLESBook:KUMAR PRAKASHANChapter:TRIANGLESExercise:EXERCISE 6.2
Explore 12 Videos
- TRIANGLESBook:KUMAR PRAKASHANChapter:TRIANGLESExercise:OBJECTIVE QUESTIONS
Explore 37 Videos
- SURFACE AREAS AND VOLUMESBook:KUMAR PRAKASHANChapter:SURFACE AREAS AND VOLUMESExercise:TEST YOUR SKILLS
Explore 5 Videos
Similar Questions
Fill in the blanks using the correct word given in brackets :
All circles are………(congruent, similar)
View SolutionIn the given figures 1 and 2, DE∣∣BC. Find the EC in 1 and AD in 2.
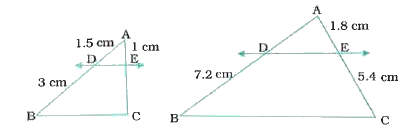
View SolutionFill in the blanks so as to make each of the following statements true :
ΔABC~ΔDEF and 2AB=DE. If BC= 8 cm, then EF=………cm.
View SolutionThe slant height of a frustum of a cone is 4 m and the perimeter of circular ends are 18 m and 16 m. Find the cost of painting its curved surface at 10 per sq. m.
View SolutionAD BE and CF are the medians of a Delta ABC .Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
View SolutionIn Figure, AD, and BE are medians of ABC and BE∣∣DF. Prove that CF=14AC.
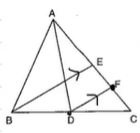
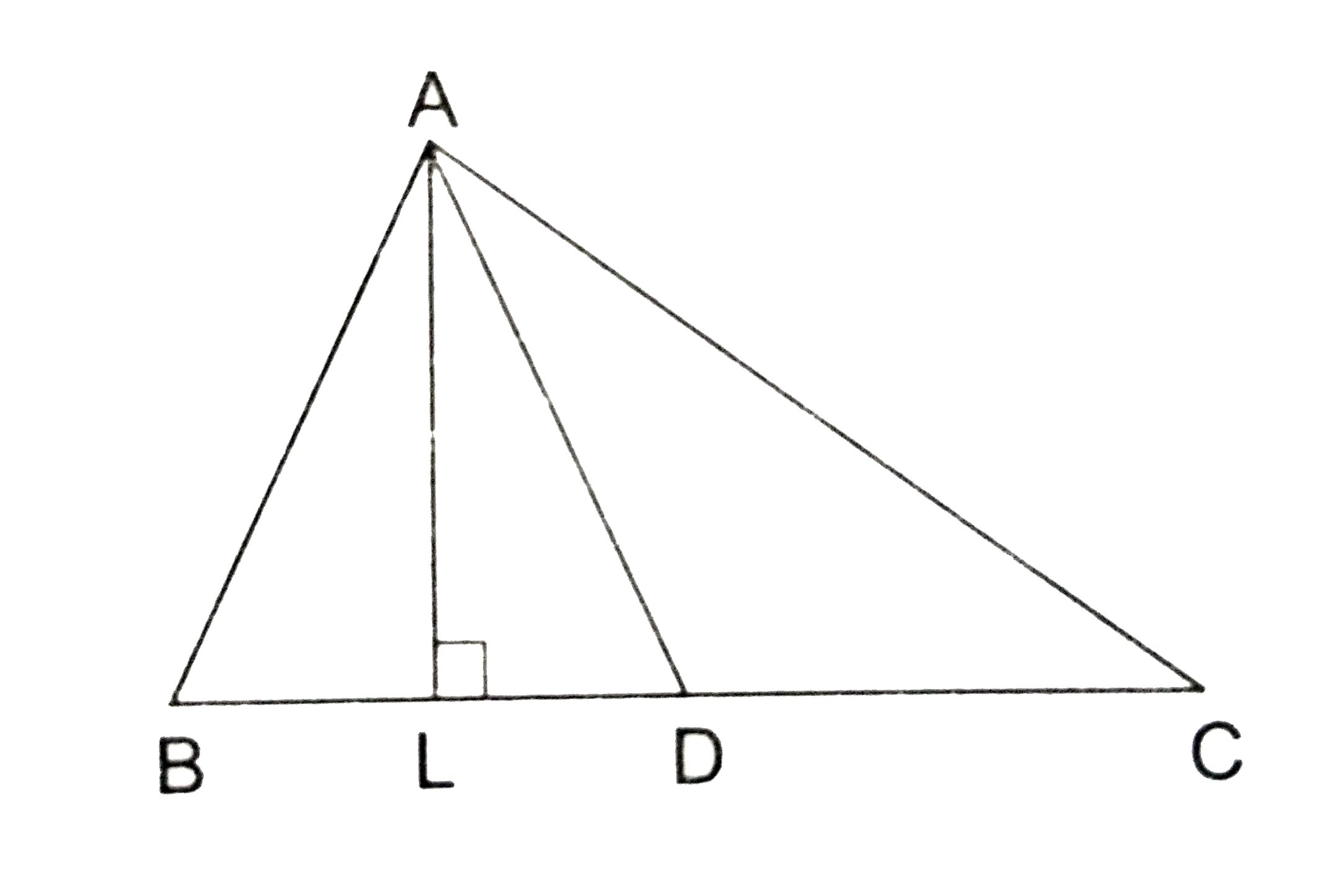
View SolutionIn aΔABC,AD is a median and AL⊥BC.
Prove that
(a) AC2=AD2+BC⋅DL+(BC2)2
(b) AB2=AD2−BC⋅DL+(BC2)2
(c) AC2+AB2=2AD2=2AD2+12BC2
View SolutionIn Figure -6 , in an equilateral triangle ABC, AD is perpendicular to BC , BE is perpendicular to AC and CF is perpendicular to AB . Prove that 4 (AD^2 +BE^2 +CF^2)=9AB^2
View SolutionIf AD, BE and CF are the medians of a ΔABC, then evaluate (AD2+BE2+CF2):(BC2+CA2+AB2).
View Solutionन्यूनकोण त्रिभुज ABC में , AD इसकी मध्यिका है सिद्ध कीजिये कि :
AD2=AB22+AC22−BC24
View SolutionIf AD, BE and CF are the medians of a ABC ,then (AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View Solution[If the AD,BE ,CF are the lengths of the medians of a △ABC then general solution of the equation ],[cosθ=√AD2+BE2+CF2AB2+BC2+CA2 is ],[ (where z is the set of all integers) ]
View SolutionIf the AD,BE,CF are the lengths of the medians of a ΔABC then general solution of the equation cosθ=√AD2+BE2+CF2AB2+BC2+CA2 is (where z is the set of all integers)
View SolutionIn the Fig. AD and BE are medians of ΔABCandBE||DF. Prove that CF=14AC.
View SolutionIn Figure -6 , in an equilateral triangle ABC, AD is perpendicular to BC , BE is perpendicular to AC and CF is perpendicular to AB . Prove that 4(AD2+BE2+CF2)=9AB2
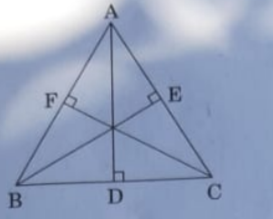
View Solution

