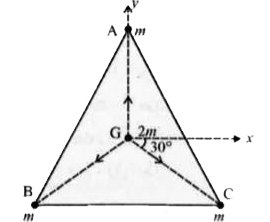
Three equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC.
(a) What is the force acting on a mass 2m placed at the centroid G of the triangle?
(b) What is the force if the mass at the vertex A is doubled ?
Take AG = BG = CG = 1 mSolution in Tamil
(a) The angle between GC and the positive x-axis is 30∘ and so is the angle between GB and the negative x-axis. The individual forces in vector notation are
FGA=Gm(2m)1ˆj
FGB=Gm(2m)1(−ˆicos30∘−ˆjsin30∘)
FGC=Gm(2m)1(+ˆicos30∘−ˆjsin30∘)
From the principle of superposition and the law of vector addition, the resultant gravitational force FR on (2m) is
FR=FGA+FGB+FGC
FR=2Gm2ˆj+2Gm2(−ˆicos30∘−ˆjsin30∘)
+2Gm2(ˆicos30∘−ˆjsin30∘)=0
Alternatively. one expects on the basis of symmetry that the resultant force ought ot the zero.
(b) Now if the mass at vertex A is doubled then
FGA=G2m.2m1ˆj=4Gm2ˆj
FGB=FGBandFGC=FGC
FR=FGA+FGB+FGC
FR=2GM2ˆj
For the gravitational force between an extended object (like the earth) and a point mass, Eq. (8.5) is not directly applicable. Each point mass in the extended object will exert a force on the given point mass and these force will not all be in the same direction. We have to add up these forces vectorially for all the point masses in the extended object to get the total force. This is easily done using calculus. For two special cases, a simple law results when you do that :
(1) The force of attraction between a hollow spherical shell of uniform density and a point mass situated outside is just as if the entire mass of the shell is concentrated at the centre of the shell. Qualitatively this can be understood as follows: Gravitational forces caused by the various regions of the shell have components along the line joining the point mass to the centre as well as along a direction prependicular to this line. The components prependicular to this line cancel out when summing over all regions of the shell leaving only a resultant force along the line joining the point to the centre. The magnitude of this force works out to be as stated above.
(2) The force of attraction due to a hollow spherical shell of uniform density, on a point mass situated inside it is zero. Qualitatively, we can again understand this result. Various regions of the spherical shell attract the point mass inside it in various directions. These forces cancel each other completely

Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT TAMILCHAPTER - GRAVITATIONEXERCISE - EXERCISES
27 Videos
- GRAVITATIONBOOK - NCERT TAMILCHAPTER - GRAVITATIONEXERCISE - ADDITIONAL EXERCISES
4 Videos
- APPENDIX 1BOOK - NCERT TAMILCHAPTER - APPENDIX 1EXERCISE - SOLVED EXAMPLE UNIT-5
14 Videos
- HEAT AND THERMODYNAMICSBOOK - NCERT TAMILCHAPTER - HEAT AND THERMODYNAMICSEXERCISE - EVALUATION (Numerical Problems)
13 Videos
Similar Questions
You can shled a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means ?
View SolutionAs you have learnt in the text, a geostationary satellite orbits the earth at a height of nearly 36,000 km from the surface of the earth. What is the potential due to earth’s gravity at the site of this satellite ? (Take the potential energy at infinity to be zero). Mass of the earth =6.0×1024kg. radius=6400km .
View SolutionThree particles of masses m1=1kg,m2=2kgandm3=3kg are placed at the corners of an equilateral triangle of side 1m as shown in Figure. Find the position of center of mass.
View SolutionCalculate the number of moles of air is in the inflated balloon at room temperature as shown in the figure

The radius of the balloon is 10 cm, and pressure inside the balloon is 180 kPa.
View Solutionकिसी समबाहु त्रिभुज ABC के प्रत्येक शीर्ष पर m kg के तीन समान द्रव्यमान रखे हैं।
(a) इस त्रिभुज के केन्द्रक G पर रखे 2m kg के द्रव्यमान पर कितना बल आरोपित हो रहा है?
(b) यदि शीर्ष A पर रखे द्रव्यमान को दो गुना कर दिया जाए, तो कितना बल आरोपित होगा ?
AG=BG=CG=1m लीजिए
View SolutionThree equal masses 2m each are placed at the vertices an equilateral triangle PQR (i) What is the force acting on a mass m placed at the centroid G of the triangle ? (ii) What is the force on mass m if the mass at the vertex P is quadrupled ? Take PG = QG = RG = 1m
View Solutionकिसी समबाहु त्रिभुज ABC के प्रत्येक शीर्ष पर mkg के तीन समान द्रव्यमान रखे हैं ।
( b ) यदि शीर्ष a पर रखे द्रव्यमान को दो गुना कर दिया जाए , तो कितना बल लगेगा ?
AG=BG=CG=1m लीजिए ।
View Solutionकिसी समबाहु त्रिभुज ABC के प्रत्येक शीर्ष पर m kg के तीन समान द्रव्यमान रखे हैं।
(a) इस त्रिभुज के केन्द्रक G पर रखे 2m kg के द्रव्यमान पर कितना बल आरोपित हो रहा है?
(b)यदि शीर्ष A पर रखे द्रव्यमान को दोगुना कर दिया जाये, | तो कितना बल आरोपित होगा? AG = BG = CG = 1 m लीजिए। (देखिए चित्र)
View SolutionThree particles, each of mass m, are placed at the vertices of an equilateral triangle. What is the force acting on a particle of mass 2m placed at the centroid D of the triangle ?
View Solutionकिसी समबाहु त्रिभुज ABC के प्रत्येक शीर्ष पर m kg तीन समान द्रव्यमान रखे है।
(a) इस त्रिभुज के केन्द्रक G पर रखे 2m kg के द्रव्यमान पर कितना बल आरोपित हो रहा है ?
(b) यदि शीर्ष A पर रखे द्रव्यमान को दो गुना कर दिया जाए, तो कितना बल आरोपित होगा ?
AG=BG=CG=1m लीजिए (देखिए चित्र)
View SolutionThree equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC. (a) What is the force acting on a mass 2m placed at the centroid G of the triangle? (b) What is the force if the mass at the vertex A is doubled ? Take AG = BG = CG = 1 m
View SolutionThree equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC. (a) What is the force acting on a mass 2m placed at the centroid G of the triangle? (b) What is the force if the mass at the vertex A is doubled ? Take AG = BG = CG = 1 m
View SolutionThree equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC . a. What is the force acting on a mass 2m placed at the centroid G of the triangle? b. What is the force if the mass at the vertex A is doubled? Take AG=BG=CG=1m
View SolutionThree equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC. (a) What is the force acting on a mass 2 m placed at the centroid G of the triangle ? (b) What is the force if the mass at the vertex A is doubled ? (Take AG = BG = CG = 1 m )
View SolutionThree equal masses of m kg each are fixed at the vetrices of an equilateral triangle ABC
(a) What is the force acting on a mass 2m placed at the centriod G of the triangle.
(b) What is the force if the mass at the vertex A is doubled ? Take AG = BG = 1m
View Solution
