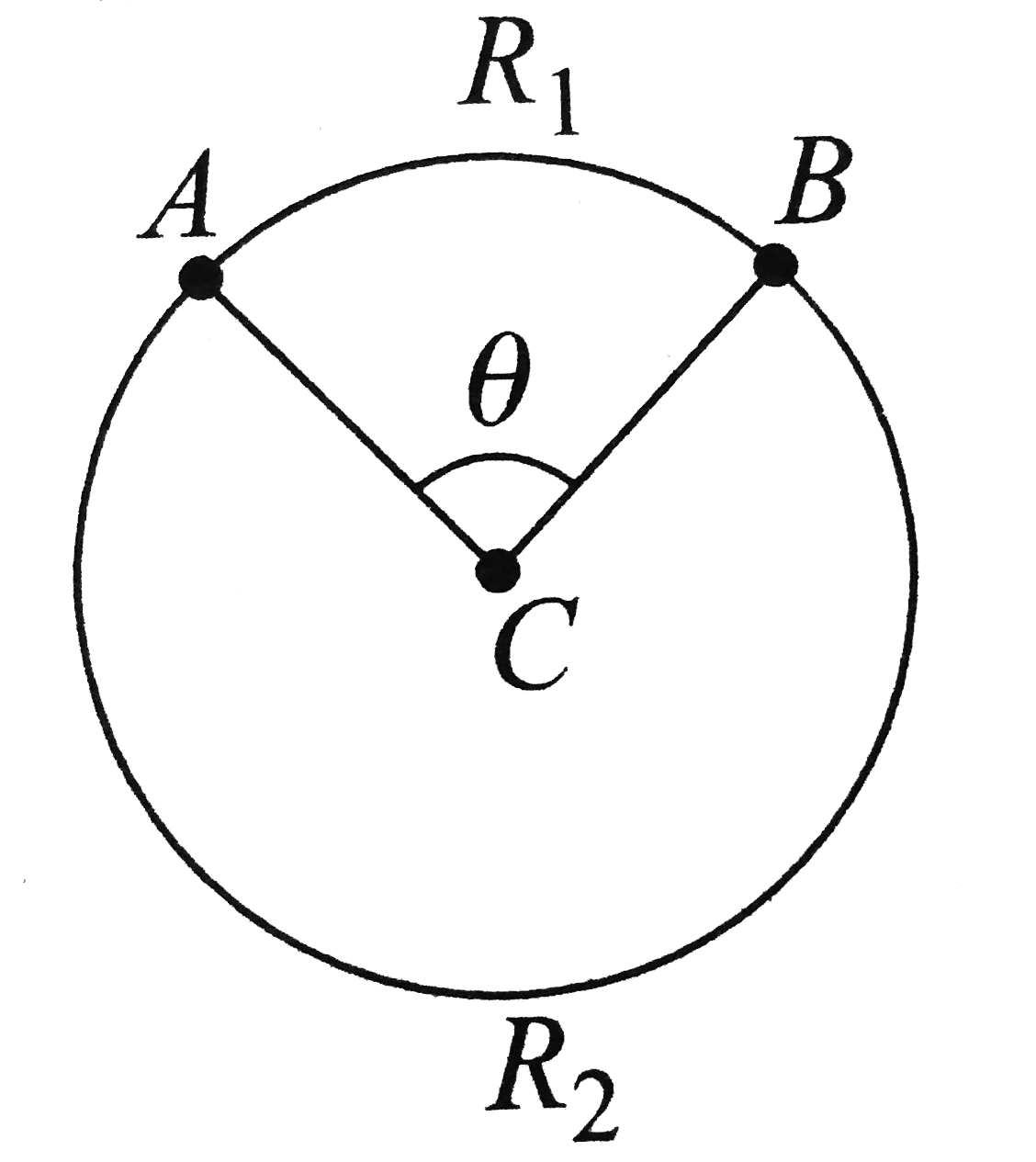
A and B are two points on a uniform metal ring whose centre is C. The angle ACB=θ. A and B are maintained at two different constant temperatures. When θ=1800, the rate of total heat flow from A to B is 1.2 W. When θ=900, this rate will be Solution in Telugu
0.6 W
0.9 W
1.6 W
1.8 W
The correct Answer is:C
Step by step video, text & image solution for A and B are two points on a uniform metal ring whose centre is C. The angle ACB=theta. A and B are maintained at two different constant temperatures. When theta=180^(0), the rate of total heat flow from A to B is 1.2 W. When theta=90^(0), this rate will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRANSMISSION OF HEATBook:AAKASH SERIESChapter:TRANSMISSION OF HEATExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II (LECTURE SHEET (ADVANCED)) Straight Objective Type Questions
Explore 6 Videos
- TRANSMISSION OF HEATBook:AAKASH SERIESChapter:TRANSMISSION OF HEATExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II (LECTURE SHEET (ADVANCED)) More than One correct answer Type Questions
Explore 4 Videos
- TRANSMISSION OF HEATBook:AAKASH SERIESChapter:TRANSMISSION OF HEATExercise:PRACTICE SHEET (EXERCISE-II) Thermal Conduction (LEVEL-II) Integer Type Questions
Explore 2 Videos
- TRANSMISSION OF HEAT Book:AAKASH SERIESChapter:TRANSMISSION OF HEAT Exercise:QUESTION FOR DESCRIPTIVE ANSWER
Explore 4 Videos
- UNITS AND MEASUREMENTBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTExercise:Practice Exercise
Explore 45 Videos
Similar Questions
The thickness of ice in a lake is 10 cm and its temperature is −100C. The thermal conductivity of ice = 0.004 cal cm−1 sec−10C−1. Density of ice = 0.92 g/cc, latent heat of ice = 80 cal/g. The time taken for thickness of ice to be doubled is
View SolutionFor transmission of heat from one place to the otther, medium is required in
View SolutionAn object is being heated by a heater supplying 60 W heat. Temperature of surrounding is 200C and the temperature of object becomes constant at 500C. Now the heater is switched off. The rate at which the object will lose heat when its temperature has dropped to 300C is 4×z watt. Then z is equal to ......................
View SolutionSolid copper cube of edge 1 cm is suspended in an evacuated enclosure . Its temperature is found to fall from 100∘C to 99∘C in 100 seconds . Another solid copper cube of edge 2cm with similar surface nature is suspended in similar manner . Find the time required for this cube to cool from 100∘C to 99∘C
View SolutionThe ratio of S.I. unit of universal gravitational constant to C.G.S. unit is
View SolutionIf θ is the angle between two vectors →a and →b, then →a⋅→b≥0 only when
(A) 0<θ<π2
(B) 0≤θ≤π2
(C) 0<θ<π
(D)0≤θ≤π
View SolutionLet f(θ)=sinθ(sinθ+sin3θ). Then f(θ) is (a)≥0 only when θ≥0 (b) ≤0 for all real θ (c)≥0 for all real θ (d) ≤0 only when θ≤0
View SolutionIn a uniform ring of resistance R there are two points A and B such that /_ ACB = theta , where C is the centre of the ring. The equivalent resistance between A and B is
View SolutionA and B are two points on uniform metal ring whose centre is O The angle AOB =theta A and B are maintaind at two different constant temperatures When theta =180^(@) the rate of total heat flow from A to B is 1.2W When theta =90^(@) this rate will be .
View SolutionA uniform metal ring with centre C have two points A and B such that angle ACB is θ. A and B are maintained at two different constant temperature.
If the angle between A and B i.e. θ=180∘ the rate of heat flow from A andB is 1.2W, then what will be the rate, when θ=90∘?
View SolutionProve that cos(900+θ)sec(−θ)tan(1800−θ)sec(3600−θ)sin(1800+θ)cot(900−θ)=−1
View SolutionProve that: tan(900−θ)sec(1800−θ)sin(−θ)sin(1800+θ)cot(3600−θ)cosec(900−θ)=1
View SolutionA and B are two points on a uniform metal ring whose centre is O. The angle AOB = theta A and B are maintained at two different constant temperatures. When theta=180^(@) , the rate of total heat flow from A to B is 1.2W. When theta=90^(@) this rate will be
View SolutionA and B are two points on a uniform metal ring whose centre is C. The angle ACB=θ. A and B are maintained at two different constant temperatures. When θ=1800, the rate of total heat flow from A to B is 1.2 W. When θ=900, this rate will be
View SolutionIn a uniform ring of resistance R there are two points A and B such that ∠ACB=θ, where C is the centre of the ring. The equivalent resistance between A and B is
View Solution

