Two particles of equal mass move in a circle of radius r under the action of their mutual gravitational attraction. Find the speed of each particle if its mass is m.Solution in Telugu
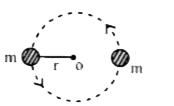
The particle will always remain diametrically opposite, so that the force on each particle will be directed along the radius.
When each particle is describing a circular orbit, the gravitational force on one of the particles must be equal to the necessary centripetal force.
mV2r=Gmm(2r)2 i.e., V=√Gm4r
Topper's Solved these Questions
- GRAVITATIONBook:AAKASH SERIESChapter:GRAVITATIONExercise:Exercise-I
Explore 124 Videos
- GRAVITATIONBook:AAKASH SERIESChapter:GRAVITATIONExercise:Exercise-II
Explore 78 Videos
- GAUSS.S LAW Book:AAKASH SERIESChapter:GAUSS.S LAW Exercise:PROBLEMS (LEVEL - II)
Explore 12 Videos
- GRAVITATIONALBook:AAKASH SERIESChapter:GRAVITATIONALExercise:EXERCISE -3
Explore 154 Videos
Similar Questions
According to Kepler, the period of revolution of a planet (T) and its mean distance from the Sun (R) are related by the equation
View SolutionA planet revolves round the sun in an elliptical orbit of minor and major axes x and y respectively . Then the time period of revolution is proportional to
View SolutionA charge q is placed at the centre of the open end of a cyclindrical vessel. Find the flux of the electric through the surface of the vessel.
View SolutionA satellite takes 1/8 years to move round the earth in its permissible orbit of radius R. The period when it revolves round the earth in an orbit of radius '2R' is
View SolutionTwo particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.
View SolutionTwo particles of equal mass m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is
View SolutionTwo particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
View SolutionTwo particles of equal mass m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is
View SolutionTwo particles of equal mass m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is
View SolutionTwo particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionFour particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles of equal mass move in a circle of radius r under the action of their mutual gravitational attraction. Find the speed of each particle if its mass is m.
View SolutionTwo particles of equal mass move in a circle of radius r under the action of their mutual gravitational attraction . Find the speed of each particle if its mass is m.
View SolutionTwo particles of equal mass move in a circle of radius r under the action of their mutual gravitational attraction. Find the speed of each particle it its mass is m.
View Solution

