In cyclic quadrilateral ABCD,∠CAB=30∘ and ∠ABC=100∘ Then,∠ADB=
50∘
100∘
75∘
60∘
The correct Answer is:A
To find the angle ∠ADB in the cyclic quadrilateral ABCD, we can follow these steps:
Step 1: Identify the Given Angles
We are given:
- ∠CAB=30∘
- ∠ABC=100∘
Step 2: Use the Triangle Angle Sum Property
In triangle ABC, the sum of the angles is 180∘. Therefore, we can write the equation:
∠CAB+∠ABC+∠ACB=180∘
Substituting the known angles:
30∘+100∘+∠ACB=180∘
Step 3: Solve for ∠ACB
Now, simplify the equation:
130∘+∠ACB=180∘
Subtract 130∘ from both sides:
∠ACB=180∘−130∘=50∘
Step 4: Use the Cyclic Quadrilateral Property
In a cyclic quadrilateral, the angles subtended by the same chord are equal. Therefore, we have:
∠ACB=∠ADB
Since we found ∠ACB=50∘, we can conclude:
∠ADB=50∘
Final Answer
Thus, the measure of ∠ADB is 50∘.
---
We are given:
- ∠CAB=30∘
- ∠ABC=100∘
In triangle ABC, the sum of the angles is 180∘. Therefore, we can write the equation:
∠CAB+∠ABC+∠ACB=180∘
Substituting the known angles:
30∘+100∘+∠ACB=180∘
Now, simplify the equation:
130∘+∠ACB=180∘
Subtract 130∘ from both sides:
∠ACB=180∘−130∘=50∘
In a cyclic quadrilateral, the angles subtended by the same chord are equal. Therefore, we have:
∠ACB=∠ADB
Since we found ∠ACB=50∘, we can conclude:
∠ADB=50∘
Thus, the measure of ∠ADB is 50∘.
Topper's Solved these Questions
- CIRCLES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - SUM TO ENRICH REMAMBER
6 Videos
- CIRCLES BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLES EXERCISE - SKILL TESTING EXERCISE
11 Videos
- INTRODUCTION TO EUCLID.S GEOMETRYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS
3 Videos
Similar Questions
Knowledge Check
In cyclic quadrilateral ABCD, ∠A=70∘and∠B+∠C=160∘. Then,∠B= ………
A35∘B25∘C50∘D130∘In cyclic quadrilateral ABCD,∠A−∠C=20∘. Then,∠A= ..........
A20∘B80∘C100∘D50∘The point of intersection for the diagonals AC and BD of the cyclic quadrilateral ABC is P. If ∠APB=64∘ and ∠CBD=28∘, the measure of ∠ADB is
A32∘B36∘C56∘D28∘
In cyclic quadrilateral ABCD, AD∣∣BC. Prove that AB = CD.
View SolutionIn the given diagram ABCD is a cyclic quadrilateral ∠OCB=50∘ and ∠BOC=110∘ Find the value of ∠DAO :

View SolutionIn the given figure, ABCD is cyclic quadrilateral. If ∠BCD=110∘and∠ABD=60∘ measures of ∠DAEand∠ADB.
View SolutionIn a given fig. ABCD is a cyclic quadrilateral with ∠BAD=100∘,∠ADC=85∘,∠ABC=x∘and∠DCB=y∘ Find x and y.
View Solution□ABCD is a cyclic quadrilateral, m (arc ABC) =220∘ then find ∠ABC,∠CDA and ∠CBE
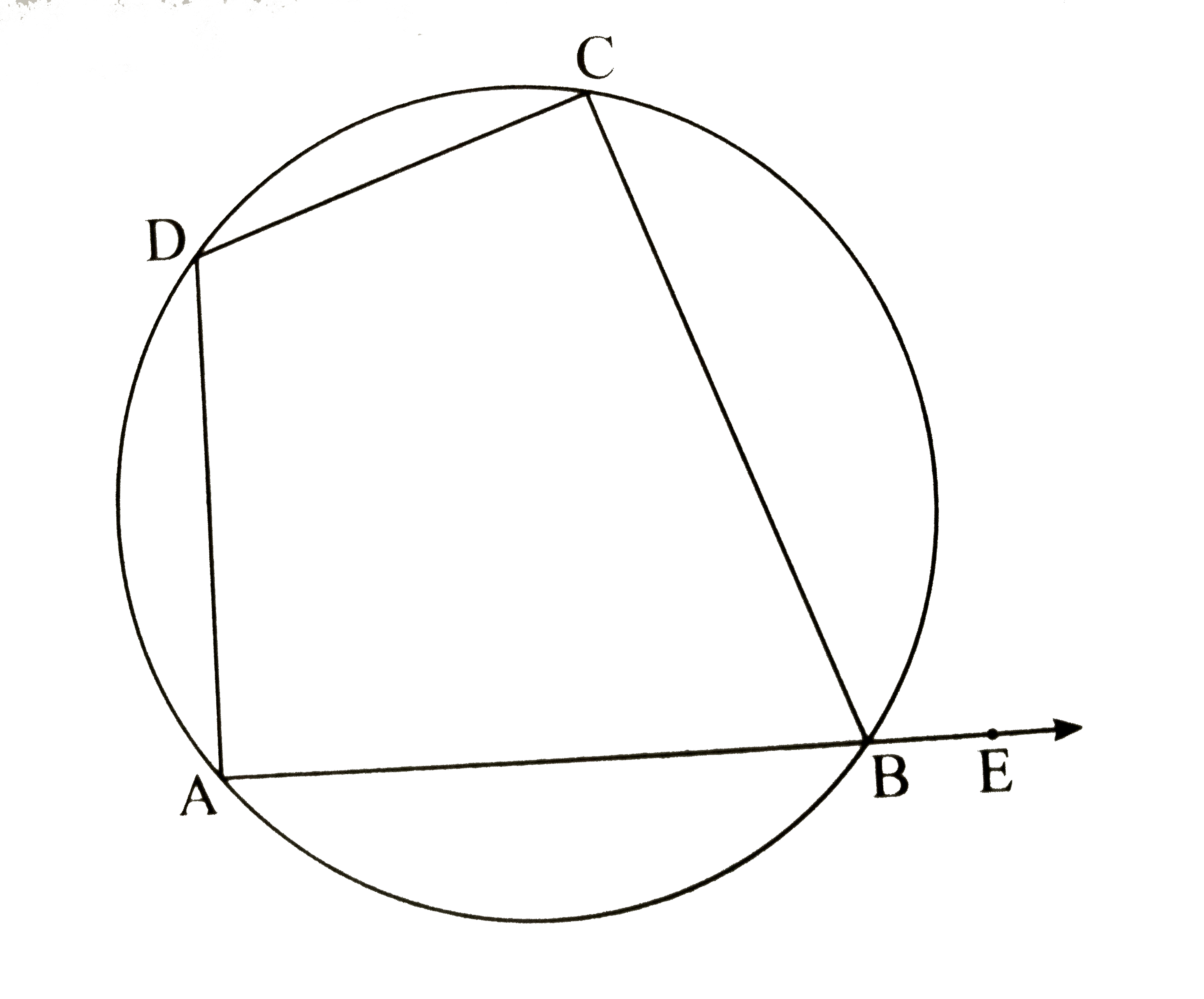
View Solution
