Ray AX is the bisector of ∠BAC and ray AY is the bisector of ∠XAC. If ∠BAY=60∘, find ∠BAC.
The correct Answer is:∠BAC=80∘
To solve the problem step by step, we will follow the logical deductions based on the information provided in the question.
1. Understanding the Angles:
- Let the measure of angle BAC be x.
- Since ray AX is the bisector of angle BAC, it divides BAC into two equal parts. Therefore, ∠BAX=x2 and ∠XAC=x2.
2. Identifying the Second Bisector:
- Ray AY is the bisector of angle XAC. Since ∠XAC=x2, ray AY divides this angle into two equal parts:
- ∠XAY=12×x2=x4
- Therefore, ∠YAC=x4 as well.
3. Setting Up the Equation:
- We know from the problem that ∠BAY=60∘.
- We can express ∠BAY in terms of x:
∠BAY=∠BAX+∠XAY=x2+x4
4. Finding a Common Denominator:
- To add x2 and x4, we need a common denominator. The least common multiple of 2 and 4 is 4:
x2=2x4
- Now we can add:
∠BAY=2x4+x4=3x4
5. Setting Up the Equation:
- Since we know ∠BAY=60∘, we can set up the equation:
3x4=60
6. Solving for x:
- To solve for x, multiply both sides by 4:
3x=240
- Now, divide both sides by 3:
x=2403=80
7. Conclusion:
- Therefore, the measure of angle BAC is:
∠BAC=x=80∘
Final Answer:
∠BAC=80∘
- Let the measure of angle BAC be x.
- Since ray AX is the bisector of angle BAC, it divides BAC into two equal parts. Therefore, ∠BAX=x2 and ∠XAC=x2.
- Ray AY is the bisector of angle XAC. Since ∠XAC=x2, ray AY divides this angle into two equal parts:
- ∠XAY=12×x2=x4
- Therefore, ∠YAC=x4 as well.
- We know from the problem that ∠BAY=60∘.
- We can express ∠BAY in terms of x:
∠BAY=∠BAX+∠XAY=x2+x4
- To add x2 and x4, we need a common denominator. The least common multiple of 2 and 4 is 4:
x2=2x4
- Now we can add:
∠BAY=2x4+x4=3x4
- Since we know ∠BAY=60∘, we can set up the equation:
3x4=60
- To solve for x, multiply both sides by 4:
3x=240
- Now, divide both sides by 3:
x=2403=80
- Therefore, the measure of angle BAC is:
∠BAC=x=80∘
∠BAC=80∘
Topper's Solved these Questions
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Multiple Choice Questions MCQs)
10 Videos
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Sums of Enrich Remember.s
8 Videos
- INTRODUCTION TO EUCLID.S GEOMETRYBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - INTRODUCTION TO EUCLID.S GEOMETRYEXERCISE - MULTIPLE CHOICE QUESTIONS
3 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Multiple Choice Questions (MCQs)
10 Videos
Similar Questions
Knowledge Check
In triangle ABC, AD⊥BC and AO is the bisector of ∠BAC. If ∠ABC=65∘and∠ACB=231∘2 , then ∠DAO is ____ (in degrees)
A201∘4B201∘5C201∘2D203∘4In the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
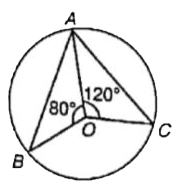 A120∘B80∘C100∘Dnone of the above
A120∘B80∘C100∘Dnone of the aboveIn the adjacent figure, the bisectors of ∠Aand∠B meet in a point P. If ∠C=100∘and∠D=60∘, find the measure of ∠APB.
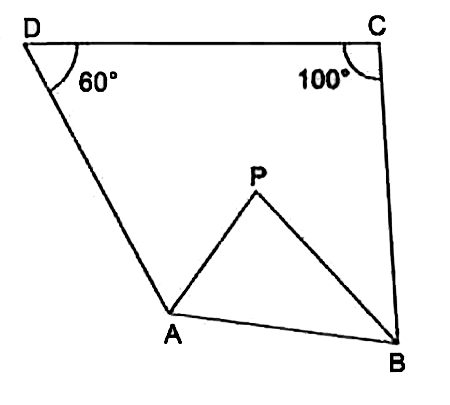 A80∘B100∘C70∘D60∘
A80∘B100∘C70∘D60∘
O is orthocentre of ΔABC if ∠BOC=120∘ find ∠BAC
View SolutionRay BD is the angle bisector of ∠ABC. The perimeter of ΔABC is
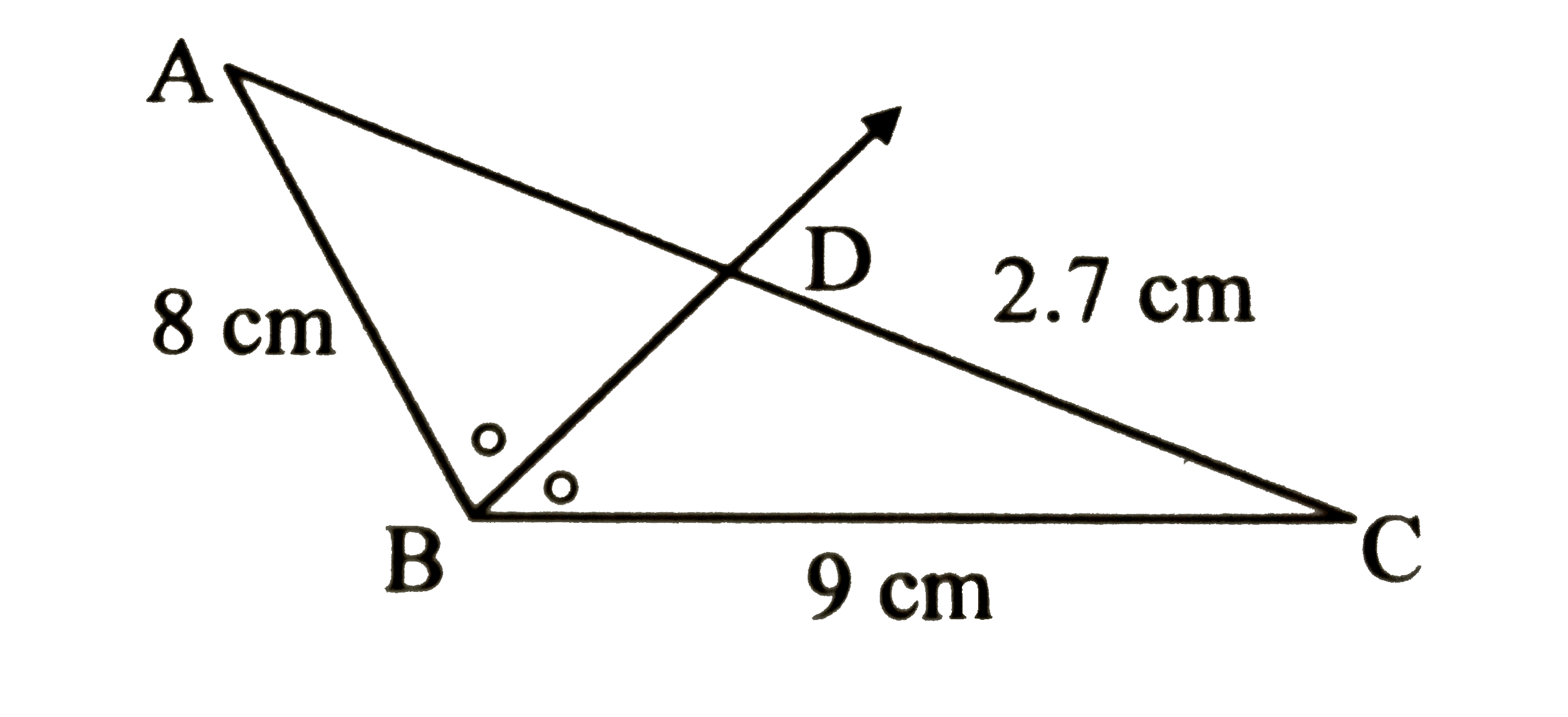
View SolutionIn a triangle ABC, AD is the angle bisector of ∠BACand∠BAD=60∘ What is the length DA?
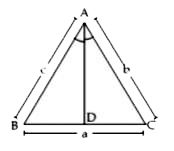
View SolutionIn ΔABC exterior angle bisectors of ∠Band∠C meets at point P if ∠BAC=80∘ then find ∠BPC.
View SolutionIn the given figure, ray OC is the bisector of ∠AOB and OD is the ray opposite to OC. Show that ∠AOD=∠BOD.

View Solution

