∠A and ∠B are complementary angles. If ∠A=x+20∘ and ∠B=x−10∘, find ∠A and ∠B.
The correct Answer is:∠A=60∘,∠B=30∘
To solve the problem, we need to find the measures of angle A and angle B, given that they are complementary angles. Here are the steps to solve the question:
Step 1: Understand the definition of complementary angles.
Complementary angles are two angles whose sum is 90 degrees.
Step 2: Write down the expressions for angle A and angle B.
We are given:
- Angle A = x + 20°
- Angle B = x - 10°
Step 3: Set up the equation based on the property of complementary angles.
Since angle A and angle B are complementary, we can write the equation:
Angle A+Angle B=90°
Substituting the expressions for angle A and angle B:
(x+20°)+(x−10°)=90°
Step 4: Simplify the equation.
Combine like terms:
x+x+20°−10°=90°
This simplifies to:
2x+10°=90°
Step 5: Solve for x.
To isolate x, subtract 10° from both sides:
2x=90°−10°
2x=80°
Now, divide both sides by 2:
x=80°2
x=40°
Step 6: Find the measure of angle A.
Now that we have the value of x, we can find angle A:
Angle A=x+20°=40°+20°=60°
Step 7: Find the measure of angle B.
Now, we can find angle B:
Angle B=x−10°=40°−10°=30°
Step 8: Conclusion.
Thus, the measures of angle A and angle B are:
- Angle A = 60°
- Angle B = 30°
Verification:
To verify, we can check if the sum of angle A and angle B equals 90°:
60°+30°=90°
This confirms that our solution is correct.
---
Complementary angles are two angles whose sum is 90 degrees.
We are given:
- Angle A = x + 20°
- Angle B = x - 10°
Since angle A and angle B are complementary, we can write the equation:
Angle A+Angle B=90°
Substituting the expressions for angle A and angle B:
(x+20°)+(x−10°)=90°
Combine like terms:
x+x+20°−10°=90°
This simplifies to:
2x+10°=90°
To isolate x, subtract 10° from both sides:
2x=90°−10°
2x=80°
Now, divide both sides by 2:
x=80°2
x=40°
Now that we have the value of x, we can find angle A:
Angle A=x+20°=40°+20°=60°
Now, we can find angle B:
Angle B=x−10°=40°−10°=30°
Thus, the measures of angle A and angle B are:
- Angle A = 60°
- Angle B = 30°
To verify, we can check if the sum of angle A and angle B equals 90°:
60°+30°=90°
This confirms that our solution is correct.
Topper's Solved these Questions
- LINE AND ANGLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:LINE AND ANGLESExercise:Multiple Choice Questions MCQs)
Explore 10 Videos
- LINE AND ANGLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:LINE AND ANGLESExercise:Sums of Enrich Remember.s
Explore 8 Videos
- INTRODUCTION TO EUCLID.S GEOMETRYBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:INTRODUCTION TO EUCLID.S GEOMETRYExercise:MULTIPLE CHOICE QUESTIONS
Explore 3 Videos
- PROBABILITY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PROBABILITY Exercise:Multiple Choice Questions (MCQs)
Explore 10 Videos
Similar Questions
Knowledge Check
In the adjacent figure, the bisectors of ∠Aand∠B meet in a point P. If ∠C=100∘and∠D=60∘, find the measure of ∠APB.
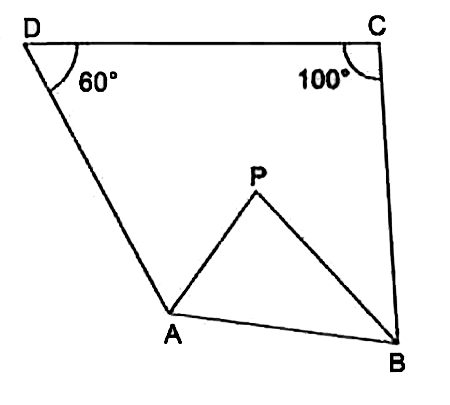 A80∘B100∘C70∘D60∘
A80∘B100∘C70∘D60∘In ΔABC,if ∠A+∠B=180∘and∠B+∠C=130∘,find ∠A,∠Band∠C.
A∠A=45∘,∠B=58∘,∠C=72∘B∠A=50∘,∠B=58∘,∠C=75∘C∠A=50∘,∠B=58∘,∠C=72∘D∠A=50∘,∠B=48∘,∠C=72∘
∠Aand∠B are two complementary angles. If ∠A is 20∘ more than ∠B, then find the angles of ∠Aand∠B.
View SolutionIn a △ABC if ∠A=72∘ and ∠B=63∘,find ∠C
View SolutionGiven that ∠A and ∠B are supplementary angles. If ∠A:∠B=7:8, then find ∠A and ∠B.
View SolutionIf ∠A and ∠B are supplementary angles. If 4∠A=5∠B, then find ∠A and ∠B.
View SolutionIn △ABC,∠A=76∘,∠B=48∘, then find ∠C=?
View SolutionIn an isosceles ΔABC if ∠A=90∘ and AB=AC, find ∠B and ∠C.
View Solution
