A particle mass m is revolving around a planet in a circular orbit of radius R. A the instant the particle have velocity 1V, another particle of mass m4 collides perfectly inelastically with the first particle. If the combine body - wasfound to follow elliptical path with velocity 51V8 then the velocity of second particle just before collision is : (∣∣∣1V∣∣∣=V)
7V8 in direction of first particle
7V8 in opposite direction of first particle
5V8in direction of first particle
5V8 in direction opposite to first particle
The correct Answer is:B
Let the velocity of first particle be x
on conserving momentum
⇒mV+m4x=(m+m4)(5V8)⇒mV+mx4=5m4×5V8
⇒mx4=25mV32−mV⇒mx4=−7mV32⇒x=−7V8
Similar Questions
Knowledge Check
A particle of mass m is revolving around a planet in a circular orbit of radius R. At the instant the particle has velocity →V another particle of mass m2 moving at velocity →v2 collides perfectly in-elastically with the first particle. The new path of the combined body will take is
ACircularBEllipticalCStraight lineDFall directly below on the groundA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
A34μ2B38μ2C14μ2D18μ2A particle moving in a circular path of radius (r) with velocity (V), Then centripetal acceleration of the particle is
AV2rBrV2CVrDV2r
Two particles of same mass m moving with velocities u1 and u2 collide perfectly inelastically. The loss of energy would be :
View SolutionIf a particle of mass 1 gm is moving along a circular path of radius 1 m with a velocity of 1 m/s, then the its angular momentum is
View SolutionA particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
View SolutionA particle (A) of mass m1 elastically collides with another stationary particle (B) of mass m2. Then :
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about P?
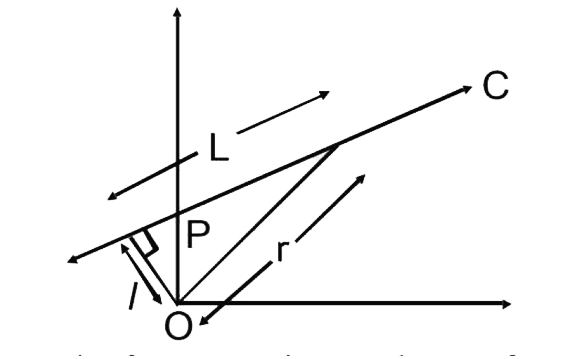
View Solution
