Consider a short bar magnet forming a magnetic dipole enclosed by an imaginary co-axial cylindrical surface with circular base area. Magnet is at the middle of cylinder. If magnetic flux through one of the circular base is phi _(0) then the magnetic flux through the other circular base will be:
A
ϕ0
B
>ϕ0
C
−ϕ0
D
<ϕ0
Video Solution
Text Solution
The correct Answer is:C
Net magnetic flux through cylinder is zero as mono-poles do not exist
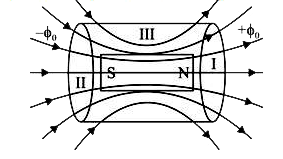
ϕnet=ϕI+ϕII+ϕIII
0+ϕ0+ϕII+0⇒ϕII=−ϕ0
|
Similar Questions
Knowledge Check
Magnetic flux through a coil depends upon
Anumber of turnsBareaCmagnetic fieldDall of theseIf the magnetic field is parallel to a surface then, the magnetic flux through the surface is
AzeroBsmall but not zeroCinfiniteDlarge but not infiniteA current carrying circular loop is placed in an infinite plane if ϕi is the magnetic flux through the inner region and ϕo is magnitude of magnetic flux through the outer region, then
AϕI>ϕoBϕI<ϕoCϕI=−ϕoDϕI=ϕo
Describe the magnetic field due to current through a circular loop.
View SolutionA circular coil, carrying a constant current i s kept in the x - y plane. The magnetic flux through the entire x - y plane exluding the area of the circular coil is given by ϕ and the magetic flux through the area of the circular coil area is given by ϕ0, then
View SolutionMagnetic field at the centre of a circular loop of area
View SolutionThe formula for induced e.m.f. in a coil due to change in magnetic flux through the coil is (here A = area of the coil, B = magnetic field)
View SolutionMagnetic field at the centre ofa circular loop of area A is B. Then magnetic moment of the loop will:
View Solution
