Consider a short bar magnet forming a magnetic dipole enclosed by an imaginary co-axial cylindrical surface with circular base area. Magnet is at the middle of cylinder. If magnetic flux through one of the circular base is phi _(0) then the magnetic flux through the other circular base will be:

A

$ϕ_{0}$

B

$> ϕ_{0}$

C

$- ϕ_{0}$

D

$< ϕ_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

magnetic flux through cylinder is zero as mono-poles do not exist.

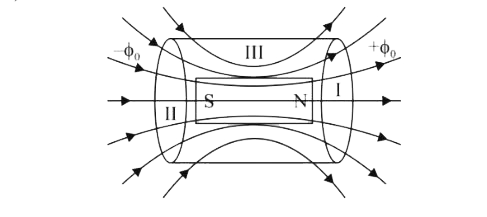
$ϕ_{r e t} = ϕ_{I} + ϕ_{I I} + ϕ_{I I I}$
$0 = ϕ_{0} + ϕ_{I I} + 0 \Rightarrow ϕ_{I I} = - ϕ_{0}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
Magnetic flux through a coil depends upon
Anumber of turns
Barea
Cmagnetic field
Dall of these
Question 2 - Select One
If the magnetic field is parallel to a surface then, the magnetic flux through the surface is
Azero
Bsmall but not zero
Cinfinite
Dlarge but not infinite
Question 3 - Select One
A current carrying circular loop is placed in an infinite plane if $ϕ$ i is the magnetic flux through the inner region and $ϕ$ o is magnitude of magnetic flux through the outer region, then
A $ϕ I > ϕ o$
B $ϕ I < ϕ o$
C $ϕ I = - ϕ o$
D $ϕ I = ϕ o$

Recommended Questions

Home
Ask Doubt
Profile