A cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. 7.35. The flywheel is mounted on a horizontal axle with frictionless bearings.
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest.
(d) Compare answers to parts (b) and (c).Solution in Gujrati

(a) Torque τ=RFsinθ
=0.2×25×sin90∘
τ=5.0Nm[∵sin90∘=1]
Moment of inertia I=MR22
=20×(0.2)22
∴I=0.4kgm2
Now Iα=τ
∴α=τI=50.4
∴α=12.5rad/s2 ....(1)
(b) Work done by the pull unwinding 2m of the cord
W=Fl
=25×2
∴W=50J
(c ) Let ω be the final angular velocity
The kinetic energy gained =12Iω2...(2)
If wheel gains angular velocity ω after starting from rest, then
Now ω2=ω20+2αθ
∴ω2=2αθ [∵ω0=0]...(3)
Angular displacement
θ=length of unwound stringradius of wheel
=20.2
∴θ=10 rad ....(4)
From eqn. (1), (3) and (4)
ω2=2alphθ
=2×12.5×10
∴ω2=250(rad s−1)2
∴ kinetic energy gained
K.=12Iω2
=12×0.4×250
∴K=50J ...(5)
(d) Equation (2) and (5) are equal, means kinetic energy gained by the wheel = work done by the force.
Here, there is no loss of energy due to friction.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-B NUMERICALS FROM TEXTUAL EXERCISE
21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-B ADDITIONAL EXERCISE
12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-A (TRY YOURSELF (VSQs))
94 Videos
- QUESTIONS ASKED IN JEE - 2020 BOOK - KUMAR PRAKASHANCHAPTER - QUESTIONS ASKED IN JEE - 2020 EXERCISE - Question
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
1 Videos
Similar Questions
Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body ?
View SolutionThe longest wavelength in Balmer series of hydrogen spectrum will be
View SolutionWhat is a rigid body ? Explain the differences between rigid body and solid body.
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionA uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is
View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
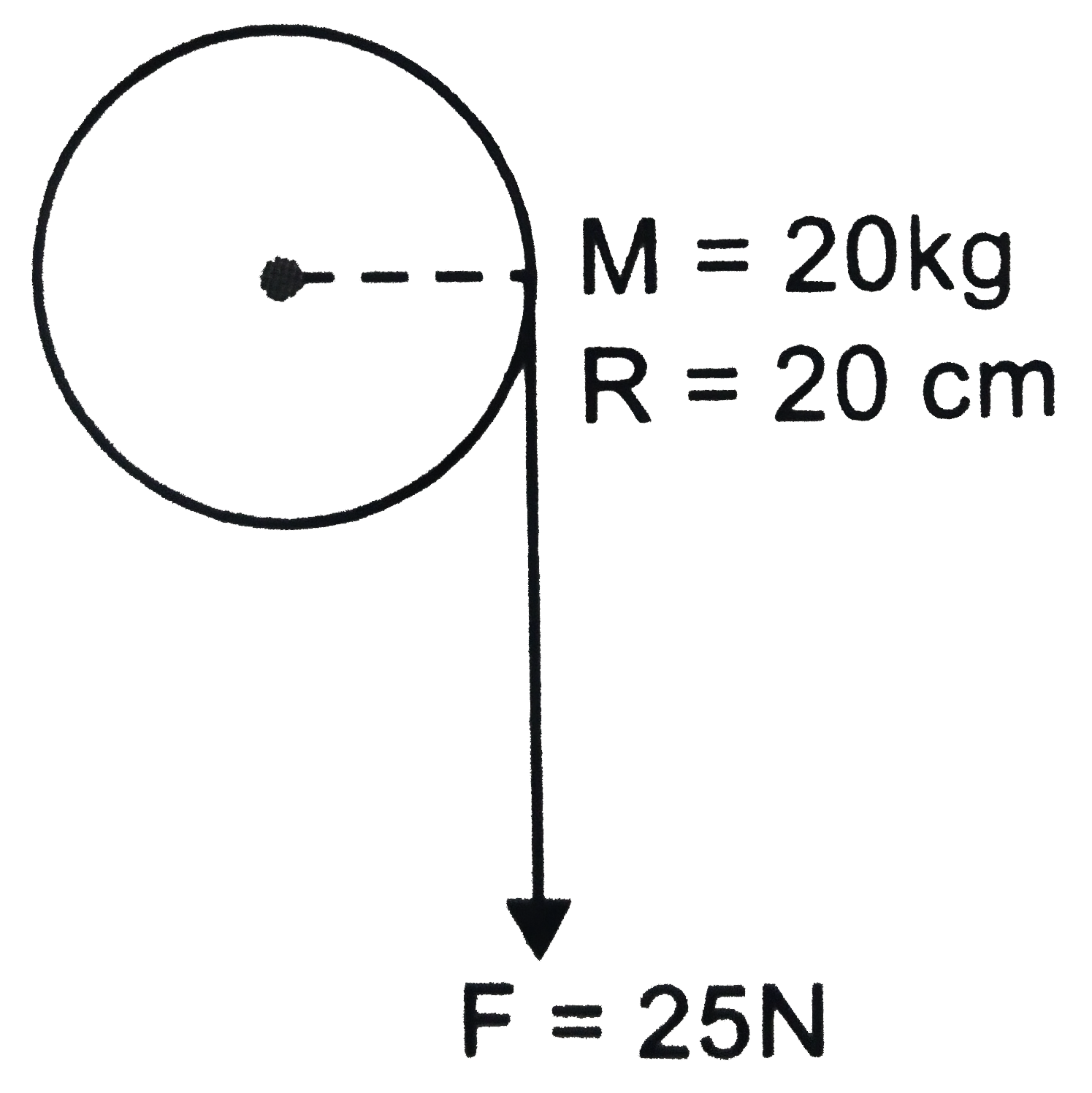
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionA string is wound round the rim of a mounted flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel in rad/s2 is
View SolutionA cord of negligible mass is wound round the rin of a flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. The work done by the pull when 2 m of the cord is unwound is
View SolutionA cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. 7.35. The flywheel is mounted on a horizontal axle with frictionless bearings.
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest.
(d) Compare answers to parts (b) and (c).
View SolutionA cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. 7.35. The flywheel is mounted on a horizontal axle with frictionless bearings. (a) Compute the angular acceleration of the wheel. (b) Find the work done by the pull, when 2m of the cord is unwound. (c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest. (d) Compare answers to parts (b) and (c).
View SolutionA cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. 7.35. The flywheel is mounted on a horizontal axle with frictionless bearings.
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest.
(d) Compare answers to parts (b) and (c).
View SolutionA cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. 7.35. The flywheel is mounted on a horizontal axle with frictionless bearings.
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest.
(d) Compare answers to parts (b) and (c).
View Solution20 cm त्रिज्या तथा 20 kg द्रव्यमान के एक गतिपालक चक्र की रिम पर एक रस्सी को लपेटा गया है। 25 N रस्सी को के बल खींचा जाता है। रस्सी के द्रव्यमान व घर्षण को नगण्य मानिये , पहिये का कोणीय त्वरण होगा
View SolutionA cord of negligible mass is wound round the rim of a fly wheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord as shown in Fig. 7.35. The flywheel is mounted on a horizontal axle with frictionless bearings.
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel starts from rest.
(d) Compare answers to parts (b) and (c).
View SolutionA string is wound round the rim of a mounted flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. Neglecting friction and mass of the string, the angular acceleration of the wheel is
View Solution
