A 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in Fig.7.27. Find the reaction forces of the wall and the floor.Solution in Gujrati
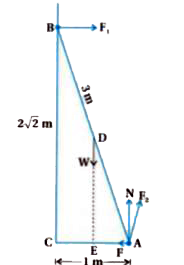
Length of ladder AB=3m
The distance of foot of ladder fro the floor AC=1m
∴ Right angle ΔACB BC=√AB2−AC2
=√(3)2−(1)2
=√8
=2√2m
The forces on the ladder are its weight W acting at its centre of gravity D.
The reaction forces F1andF2 are acting on wall and floor.
Force F2 is resolved into two components are normal reaction N and the force of friction F parallel to AC.
which prevents the ladder from sliding away from the wall and therefore directed toward the wall.
For translational equilibrium
N−W=0 (in vertical diretion)
∴N=W...(1)
Taking the forces in horizontal direction
f−F1=0
∴F1=f...(2)
For rotational equilibrium, taking moment of forces about A
F1(BC)−W(AE)=0
∴F1(2√2)−W(12)=0
∴2√2F1=W2
∴F1=W4√2....(3)
Now W=20g[∵W=mg]
=20×9.8
=196N
∴ From eqn. (1),
N=196N
From eqn. (3),
F1=1964√2
∴F1=34.65N
∴ From eqn. (2),
f=34.65N
Now in ΔANF2,
AF2=√AN2+NF22
=(√N2+f2)
=√(196)2+(34.65)2
=√38416+1200.62
=√39616.62
=199.039
∴AF2≈199N
Suppose force AF2 makes an angle α with horizontal
∴In ΔANF2,
tanα=Nf
=19634.65
=5.6565
∴α=tan−1(5.6565)
=79∘56.
∴α≈80∘
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-B NUMERICALS FROM TEXTUAL EXERCISE
Explore 21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-B ADDITIONAL EXERCISE
Explore 12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-A (TRY YOURSELF (VSQs))
Explore 94 Videos
- QUESTIONS ASKED IN JEE - 2020 Book:KUMAR PRAKASHANChapter:QUESTIONS ASKED IN JEE - 2020 Exercise:Question
Explore 16 Videos
- THERMAL PROPERTIES OF MATTERBook:KUMAR PRAKASHANChapter:THERMAL PROPERTIES OF MATTERExercise:Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
Explore 1 Video
Similar Questions
Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body ?
View SolutionThe longest wavelength in Balmer series of hydrogen spectrum will be
View SolutionWhat is a rigid body ? Explain the differences between rigid body and solid body.
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionA uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
View SolutionIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle theta with the horizontal floor. The coefficient of friction between the wall and the ladder is mu_1 and that between the floor and the ladder is mu_2. the normal reaction of the wall on the ladder is N_1 and that of the floor is N_2. if the ladder is about to slip. than
View SolutionA 3m along ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall. Find the rection forces of the wall and the floor.
View Solution20 kg द्रव्यमान की एक3m लम्बी सीढ़ी एक घर्षणविहीन दीवार के साथ झुका क्र टिकाई गई है । इसका निचला सिरा फर्श पर दीवार से 1 m की दूरी पर है । दीवार और फर्श के प्रतिक्रिया बल ज्ञात कीजिये ।
View Solution20 किग्रा द्रव्यमान की एक 3 मी. लंबी सीढ़ी एक घर्षण विहीन दीवार के साथ झुकाकर टिकाई गई है जैसा कि चित्र में दर्शाया गया है । इसका निचला सिरा फर्श पर दीवार से 1 मी. की दूरी पर है । दीवार और फर्श के प्रतिक्रिया बल ज्ञात कीजिए ।
View SolutionA 3 m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in the following figure, Find the reaction forces of the wall and the floor.
View SolutionA 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in Fig.7.27. Find the reaction forces of the wall and the floor.
View SolutionA 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in Fig.7.27. Find the reaction forces of the wall and the floor.
View SolutionA 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in Fig.7.27. Find the reaction forces of the wall and the floor.
View SolutionA 3m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in Fig.7.27. Find the reaction forces of the wall and the floor.
View SolutionA 3m along ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall. Find the rection forces of the wall and the floor.
View Solution

