If the equation |2−x|−|x+1|=k has exactly one solution, then number of integral values of k is (A) 7 (B) 5 (C) 4 (D) 3
A
7
B
5
C
4
D
3
Video Solution
Text Solution
The correct Answer is:B
Let f(x)=|x−2|−|x+1|=⎧⎪⎨⎪⎩3x<−1−2x+1−1≤x≤2−3x>2
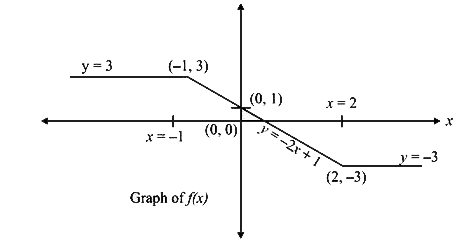
So, k∈(−3,3)<br>:. k_("integers ") =-2, -1 , 0,1,2
|
Similar Questions
Knowledge Check
If the equation ln (x2+5x)−ln(x+a+3)=0 has exactly one solution for x, then possible integral value of a is:
A−3B−1C0D2If the equation xlogax2=xk−2ak,a≠0has exactly one solution for x, then the value of k is/are
A6+4√2B2+6√3)C6−4√2D2−6√3
If cosx=k has exactly one solutions in [0,2π] , then write the values of k .
View SolutionIf the equation x4+kx2+k=0 has exactly two distinct real roots, then the smallest integral value of |k| is:
View SolutionIf the equation x2−(2k+1)x+(3k+2)=0 has exactly one root in (-1, 4), then the possible interval of the values of k is
View SolutionLet f(x)=x+2|x+1|+2|x−1|. If f(x)=k has exactly one real solution, then the value of k is (a)3 (b) 0 (c)1 (d) 2
View SolutionIf the equation x2−(2k+1)x+k+2=0 has exactly one root in (0, 2) such that maximum possible negative integral value of k is m and minimum possible positive integral value of k is M, then IM – m| is
View SolutionIf exactly one root of the equation x2+(k+1)x+5k=0 lies in (0,5) then the number of integral values of k is
View Solution
