If |x−1|+|x−2|+|x−3|=k,xεR then value of k for which given equation has exactly one solution.
Video Solution
Text Solution
The correct Answer is:2
If |x−1|+|x−2|………….
When k=2
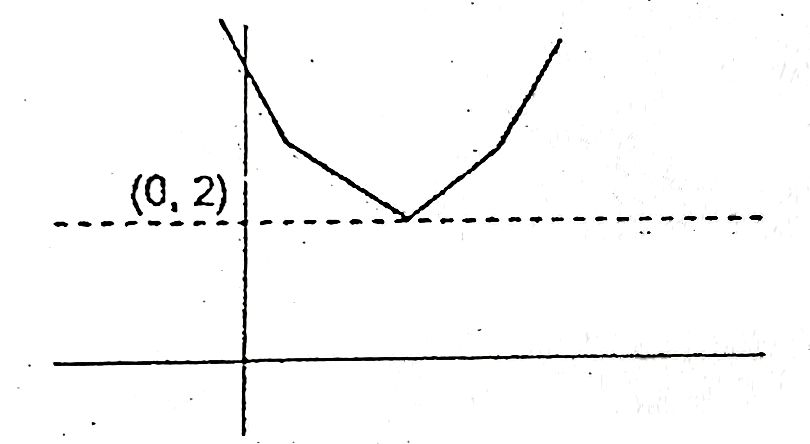
y=2 line cut the graph of
y=|x−1|+|x−2|+|x−3| at one point.
|
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART : 1MATHEMATICS SEC - 1
Explore 1 Video
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART : 1MATHEMATICS
Explore 9 Videos
- TEST PAPERBook:RESONANCEChapter:TEST PAPERExercise:CHEMISTRY
Explore 37 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:MATHEMATICS
Explore 131 Videos
Similar Questions
Knowledge Check
Minimum integral value of k for which the equation ex=kx2 has exactly three real distinct solution,
A1B2C3D4Let us consider an equation f(x)=x3−3x+k=0.then the values of k for which the equation has
Exactly one root which positive , then k belongs toA(−∞,−2)B(2,∞)C(0,2)D(−2,0)Let us consider an equation f(x)=x3−3x+k=0.then the values of k for which the equation has
Exactly one root which is negative, then k belongA(2,∞)B(0,2)C(-2,0)D(−∞,−2)
Find the no. of integral values of k for which the equation 7cosx+5sinx=2k+1 has atleast one solution.
View SolutionIf k=|x−1|+|x−2|+|x−3|+|x−4|, then minimum integral value of k for which the above equation is satisfied for exactly 2 values of x.
View SolutionThe number of integer values of k, for which the equation 2sinx=2k+1 has a solution, is
View SolutionLet f(x)=2|x|−1x−3
Range of the values of 'k' for which f(x)=k has exactly two distinct solutions:
View SolutionLet f(x)=sin−1x−cos−1, x, then the set of values of k for which of |f(x)|=k has exactly two distinct solutions is :
View Solution
