माना कि f:[0,1]→R (सभी वास्तविक संख्याओं का समुच्चय) एक फलन है। मान लीजिए फलन f दो बार अवकलनीय है f(0)=f(1)=0 तथा f(x)−2f’(x)+f(x)≥ex,xε[0,1] को संतुष्ट करता है।
यदि फलन e−xf(x), अंतराल [0,1] में अपना न्यूनतम मान x=14 पर लेता है तब निम्न में से कौन सत्य है?
f'(x)<f(x),14<x<34
f'(x)>f(x),0<x<14
f'(x)<f(x),0<x<14
f'(x)<f(x),34<x<1
The correct Answer is:C, D
Step by step video, text & image solution for माना कि f:[0,1]toR (सभी वास्तविक संख्याओं का समुच्चय) एक फलन है। मान लीजिए फलन f दो बार अवकलनीय है f(0)=f(1)=0 तथा f"(x)-2f’(x)+f(x)gee^(x),x epsilon[0,1] को संतुष्ट करता है। यदि फलन e^(-x)f(x), अंतराल [0,1] में अपना न्यूनतम मान x=1/4 पर लेता है तब निम्न में से कौन सत्य है? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( MATCH THE COLUMN TYPE)13videos
फलन, सीमा, सांतत्य तथा अवकलनीयता
- BOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( PASSAGE TYPE)9videos
फलन, सीमा, सांतत्य तथा अवकलनीयता
- BOOK - ERRORLESS HINDICHAPTER - प्रायिकताEXERCISE - EXERCISE99videos
प्रायिकता
- BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - JEE Advanced (integer type questions)8videos
लघुगणक और आंशिक भिन्नें
Similar Questions
कॉलम I में दिए गए वक्तव्यों/व्यंजकों का कॉलम II में दिये गये मानों से सुमेल करे।
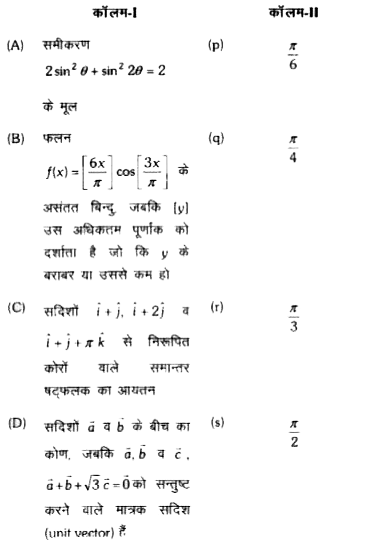 03:05View Solution
03:05View Solutionकथन-1 प्रत्येक फलन, एक सम फलन तथा एक विषम फलन के योग के रूप में अद्वितीय परिभाषित किया जा सकता है।
कथन-2 प्राचल a के मानों का समुच्चय [9,∞) है जिसके लिए फलन f(x) को f(x)=tan(sinx)+[x2a] के द्वारा समुच्चय [−3,3] में एक विषम फलन परिभाषित किया जाता है।00:53View SolutionA, B, C तीन परस्पर स्वतंत्र घटनायें हैं। S1 तथा S2 दो कथनों को देखने पर
S1 : A तथा B∪C स्वतन्त्र हैं
S2 : A तथा B∩C स्वतन्त्र हैं तब02:58View Solutionपद 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2…⎞⎟ ⎟⎠ का मान है
06:04View Solutionफलन f(x)=2sinx का आयाम है -
02:06View Solutionयदि फलन f(x) द्वारा अधिकतम मान x व y न्यूनतम मान ग्रहण किया जाता है तो इस फलन का आयाम . . . . . . . है ।
02:18View Solutionमान लीजिए कि f:[0,1]→[0,1],f(x)={x,यदि x परिमेय है1−x,यदि x अपरिमेय है द्वारा परिभाषित है , तो (fof)x:
03:20View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
02:43View Solutionयदि द्विअवकलनीय f(x) फलन x=a पर स्थानीय उच्चिष्ठ है , तो
02:12View Solutiona का न्यूनतम मान ज्ञात कीजिए कि फलन f(x)=x2+ax+5 अंतराल [1, 2] में वर्धमान है।
03:45View Solutionवह अन्तराल ज्ञात कीजिए जिसमें फलन f(x)=x−2x+1 एक वर्धमान फलन है।
06:01View Solutionसिद्ध कीजिये कि (0,2π) में फलन f(x)=x−sinx वर्धमान है।
05:11View Solutionसिद्ध कीजिये कि प्रदत फलन f(x)=cosx
(0, pi) में निरंतर हस्यमान है।01:27View Solutionएक द्विघात बहुपद f(x), जो f(0)=0,f(1)=1,f'(x)>0, को सभी x∈(0,1) के लिए संतुष्ट करता है, है
04:48View Solutionफलन f(x)=In(π+x)In(e+x) है
02:40View Solutionमाना फलन निम रूप से परिभाषित है
f(x)={sin−1λ+x2,0<x<12x,x≥1
x = 1 पर F(x) का मान निम्निष्ठ होगा, यदि λ का मान है05:23View Solution


