यदि f(x) एक धनात्मक वास्तविक मानों का फलन है जो x=a तथा x=b के लिए सममित है जहां a तथा b g(x)=√1−log3(x2−6x+11) के प्रांत (डोमेन) में क्रमशः न्यूनतम तथा अधिकतम मान है तब
S=50∑r=1f(r+p),50∏r=1f(r)=250, जहां p=2(b−a) तब S का न्यूनतम मान है
100
10
1000
2
The correct Answer is:A
Step by step video, text & image solution for यदि f(x) एक धनात्मक वास्तविक मानों का फलन है जो x=a तथा x=b के लिए सममित है जहां a तथा b g(x)=sqrt(1-log_(3)(x^(2)-6x+11)) के प्रांत (डोमेन) में क्रमशः न्यूनतम तथा अधिकतम मान है तब S=sum_(r=1)^(50)f(r+p),prod_(r=1)^(50)f(r)=2^(50), जहां p=2(b-a) तब S का न्यूनतम मान है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- फलन, सीमा, सांतत्य तथा अवकलनीयताBOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( MATCH THE COLUMN TYPE)
13 Videos
- फलन, सीमा, सांतत्य तथा अवकलनीयताBOOK - ERRORLESS HINDICHAPTER - फलन, सीमा, सांतत्य तथा अवकलनीयताEXERCISE - JEE ADVANCED( PASSAGE TYPE)
9 Videos
- प्रायिकताBOOK - ERRORLESS HINDICHAPTER - प्रायिकताEXERCISE - EXERCISE
99 Videos
- लघुगणक और आंशिक भिन्नें BOOK - ERRORLESS HINDICHAPTER - लघुगणक और आंशिक भिन्नें EXERCISE - JEE Advanced (integer type questions)
8 Videos
Similar Questions
कॉलम I में दिए गए वक्तव्यों/व्यंजकों का कॉलम II में दिये गये मानों से सुमेल करे।
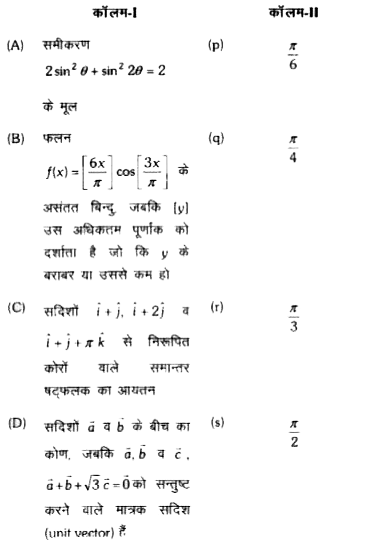
View Solutionकथन-1 प्रत्येक फलन, एक सम फलन तथा एक विषम फलन के योग के रूप में अद्वितीय परिभाषित किया जा सकता है।
कथन-2 प्राचल a के मानों का समुच्चय [9,∞) है जिसके लिए फलन f(x) को f(x)=tan(sinx)+[x2a] के द्वारा समुच्चय [−3,3] में एक विषम फलन परिभाषित किया जाता है।
View SolutionA, B, C तीन परस्पर स्वतंत्र घटनायें हैं। S1 तथा S2 दो कथनों को देखने पर
S1 : A तथा B∪C स्वतन्त्र हैं
S2 : A तथा B∩C स्वतन्त्र हैं तब
View Solutionपद 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2…⎞⎟ ⎟⎠ का मान है
View Solutionयदि फलन f(x) द्वारा अधिकतम मान x व y न्यूनतम मान ग्रहण किया जाता है तो इस फलन का आयाम . . . . . . . है ।
View Solutionx के किन मानों के लिए फलन f(x)=x1+x2 वर्धमान तथा ह्रासमान है।
View Solutionयदि y=x2+4 तथा x का मान 3 से 3.1 परिवर्तित होता है तब अवकलज के प्रयोग से y में परिवर्तनका सन्निकटन मान ज्ञात कीजिए ।
View Solutionx के किन मानो के लिए फलन f(x)=(x)(x2+1 वर्धमान तथा हस्यमान है ?
View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
View Solutionयदि x एक धनात्मक पूर्णाक है, तब Δ=∣∣ ∣ ∣∣x!(x+1)!(x+2)!(x+1)!(x+2)!(x+3)!(x+2)!(x+3)!(x+4)!∣∣ ∣ ∣∣ का मान है-
View Solutionयदि A=[logx−1−logx2] और यदि det (A)=2, तब x का मान है
View Solutionλ का वह मान जिसके लिए द्विघात समीकरण x2+(3−λ)x+2=λ के मूलों के वर्गों के योग का मान न्यूनतम है , है ?
View Solutionदिया है बहुपद f(x)=1+2x+3x2+4x3.
माना कि f(x) के भिन्न, वास्तविक मूलो का योग S है तथा t=|S| है |
Q. वास्तविक संख्या S, निम्न अन्तराल में है
View Solutionयदि log2x+logx2=103=log2y+logy2 तथा x≠y, तब x+y का मान है।
View Solutionएक फलन g जो प्रत्येक वास्तविक संख्या x>0 के लिए परिभाषित है तथा g(1)=1,g'(x2)=x3 को सभी x>0 के लिए सन्तुष्ट करता है, तो g (4) का मान है
View Solutionयदि (1+i√3)12=a+ib है a तथा b वास्तविक है तो b का मान है
View Solution