The electric potential in a region is represented as, V = 2x + 3y - z obtain expression for electric field strenght. Solution in Telugu
→E=2ˆi+3ˆj−ˆk
→E=−2ˆi−3ˆj+ˆk
→E=2ˆi−ˆj+3ˆk
→E=ˆi+2ˆi−3ˆk
The correct Answer is:B
Step by step video, text & image solution for The electric potential in a region is represented as, V = 2x + 3y - z obtain expression for electric field strenght. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTION)1videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - II (ADVANCED) LINKED COMPREHENSION TYPE QUESTION)2videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTION)19videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE6videos
ELECTROMAGNETICS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS9videos
ELEMENTS OF VECTORS
Similar Questions
A conducting sphere of radius b has spherical cavity with its centre displaced by "a" from centre of sphere, A point charge q is placed at the centre of cavity. .Q. charge is given to conducting sphere and charge qo is placed at a distance c from centre (O1) of sphere such that O1andO2andp are collinear
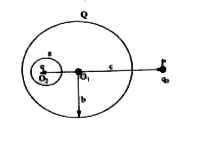 01:31View Solution
01:31View SolutionIf a charge is moving towards the centre of an earthed conducting sphere of radius b with uniform velocity v. Distance of two points A and B from centre of sphere are 3a & 2a. Conducting sphere is earthed with an ammeter and resistance in series (as shown)
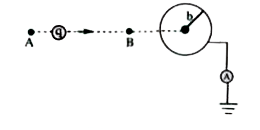
Net charge on surface of conductor at this instant01:31View SolutionLet V be electric potential and E the mangitude of the electric field. At a given position, which of the statement is true ?
02:36View SolutionWhat is the radius of the path of an electron (mass 9 × 10-31 kg and charge 1.6×x10–19 C) moving at a speed of 3×x107 m/s in a magnetic field of 6x×10−4 T perpendicular to it? What is its frequency? Calculate its energy in keV. (1eV=1.6×10−19J)
03:08View SolutionFind the components of vector ¯¯¯A=2ˆi+3ˆj along the directions of ˆi+ˆjandˆi−ˆj
04:36View SolutionThe electric potential in a region is represented a v=2x+3y−z. Obtain expression for electric field strength.
02:47View SolutionThe electric potential in a region is represented a v = 2x + 3y - z . Obtain expression for electric field strength.
03:31View SolutionElectric potential at any point is V = - 5 x + 3y + sqrt(15) z , then the magnitude of the electric field is
01:18View SolutionThe electric potential in a region is given by V = (2x^(2) - 3y) volt where x and y are in meters. The electric field intensity at a point (0, 3m, 5m) is
04:40View SolutionElectric potential at any point in a region is given as
V=5x+3y+√15z
In this region the magnitude of the electric field is:02:30View SolutionA region is specified by the potential function V=2x2+3y3−5z2. Calculate the electric field intensity at a point (2,4,5) in this region.
02:54View SolutionElectric potential in a region is given by V=12x2+3y2+z2. Calculate the electric field intensity at point (1m, 3m, 2m).
01:39View Solutionएक क्षेत्र में वैद्युत विभव निम्न प्रार दर्शाया जाता है
V=2x+3y−z
वैद्युत क्षेत्र की तीव्रता के लिए व्यंजक प्राप्त कीजिए।01:45View SolutionIn a region the electric potential is given by V = 2x + 2y -3z . Obtain the expression for electric field 0.
03:55View SolutionThe electric potential in a region is represented as
V=2x+3y−z
obtain expression for electric field strength.01:32View Solution
