The velocity of a particle under going SHM at the mean position is 2ms−1. Find the velocity of the particle at the point where the displacement from the mean position is equal to half the amplitude.Solution in Telugu
1.234ms−1
1.732ms−1
2.732ms−1
1.414ms−1
The correct Answer is:B
Step by step video, text & image solution for The velocity of a particle under going SHM at the mean position is 2ms^(-1). Find the velocity of the particle at the point where the displacement from the mean position is equal to half the amplitude. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:EXERCISE-3
Explore 49 Videos
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:PROBLEM
Explore 249 Videos
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:EXERCISE-1B
Explore 20 Videos
- OSCILLATIONBook:AAKASH SERIESChapter:OSCILLATIONExercise:QUESTIONS FOR DESCRIPTIVE ANSWERS
Explore 12 Videos
- PHYSICAL WORLDBook:AAKASH SERIESChapter:PHYSICAL WORLDExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 5 Videos
Similar Questions
The displacement of two particles executing S.H.M are represented by y1=asin(wt+ϕ) and y2=acoswt. The phase difference between the velocities of these particles is
View SolutionWhich of the following examples represent simple harmonic motion and which represent periodic but not simple harmonic motion?
View Solution(A) : All oscillatory motions are necessarily periodic motion in conservative fields but all periodic motion are not oscillatory.
(R) : Simple pendulum is an example of oscillatory motion.
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find the amplitude and the time period of the motion of the block.

View SolutionWhat is Physics ?
View SolutionVelocity at mean position of a particle executing SHM is v. Velocity of the particle at a distance equal to half of the amplitude will be
View SolutionThe velocity of particle undergoing SHM is v at the mean position. If only amplitude is doubled, the velocity at mean position
View SolutionA particle executing SHM passes through the mean position with a velocity of 4 ms^(-1) . The velocity of the particle at a point where the displacement is half of the amplitude is
View SolutionA graph between velocity and displacement of a particle performing SHM is shown. Find the acceleration when the particle is at half of maximum displacement from mean position.
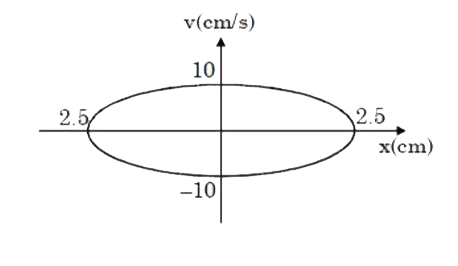
View SolutionAt a particular position the velocity of a particle in SHM with amplitude a is √3/2 that at its mean position. In this position, its displacement is :
View SolutionThe velocity of a particle in simple harmonic motion at displacement y from mean position is
View SolutionThe velocity of a particle, undergoing SHM is v at the position. If its amplitude is doubled, the velocity at the mean position will be…………….
View SolutionThe velocity of a particle under going SHM at the mean positon is 2ms^(-1) . Find the velocity of the particle at the point where the displacement form the mean position is equal to half the amplitude
View SolutionThe velocity of a particle under going SHM at the mean position is 4ms^(-1) . Find the velocity of the particle at the point where is equal to half the amplitude.
View SolutionThe velocity of a particle under going SHM at the mean positon is 2ms−1. Find the velocity of the particle at the point where the displacement form the mean position is equal to half the amplitude
View Solution

