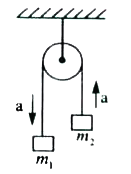
Find the acceleration of center of mass of the blocks of masses m1 and m2(m1>m2) in Atwood's machine : Solution in Telugu
We know from Newton.s laws of motion magnitude of acceleration of each block is
a=(m1−m2m1+m2)g
Now acceleration of their C.M is
acm=m1a+m2(−a)m1+m2=(m1−m2m1+m2)a
acm=(m1−m2m1+m2)(m1−m2m1+m2)g
∴ Accleration of centre of mass acm=(m1−m2m1+m2)2g
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE - 1A
120 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE - 1B
51 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
Similar Questions
Three identical spheres each of radius R are placed touching each other on a horizontal table. The centre of mass of the system is located
View Solution(A) : Position of centre of mass of a body (w.r.t body frame) is independent of co-ordinate system.
(R ) : Internal forces do not effect the motion of centre of mass.
View SolutionIf the work done in blowing a soap bubble of volume 'V' is W, then the work done in blowing a soap bubble of volume '2V' is
View SolutionA constant pressure gas thermometer has a volume of 200cc, 273.2cc and 525 .1cc at 0°C, 100°C and boiling point of sulphur respectively. The resistance possessed by a platinum wire at the same temperatures as above are 2.000Ω,2.778Ωand5.280Ω respectively. Estimate the boiling point of sulphur on the basis of the two sets of observations.
View SolutionFigure shows a block of mass m_(1) sliding on a block of mass m_(2) , with m_(1) gt m_(2) . Find the (a) acceleration of each block (b) tension in the string (c ) force exerted by m_(1) on m_(2) . ltbr> (d) force exerted by m_(2) on the incline.
View SolutionTwo block of masses m_(1) and m_(2) are connected as shown in the figure. The acceleration of the block m_(2) is:
View SolutionThree blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.
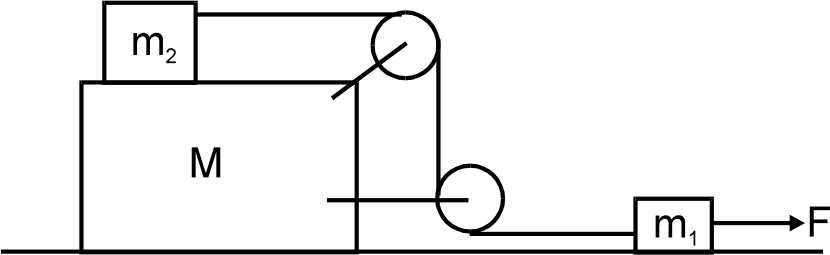
(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2
View SolutionThree block of masses m1,m2 and m3 kg are placed in contact with each other on a frictionless table. A force F is applied on the heaviest mass m1, the acceleration of m2 will be

View Solution(a) shows a block of mass m_(1) sliding on a block of mass m_(2) , with m_(1) gt m_(2) . Find (a) the acceleration of each block, (b) tension in the string, (c) force exerted by m_(1) on m_(2) (d) force exerted by m_(2) on the incline
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionIn the figure, the blocks have masses M_(1) and M_(2) (M_(1) gt M_(2)) and acceleration a. The pulley P has a radius r and some mass the string not slip on the pulley
View SolutionTwo masses m_(1) and m_(2) ( m_(2) gt m_(1)) are hanging vertically over frictionless pulley. The acceleration of the two masses is :
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View Solutionचित्र में प्रदर्शित दोनों ब्लॉकों के द्रव्यमान m1 व m2 आसमान (m2>m1) है m2 का त्वरण a नीचे की ओर है। तथा P की त्रिज्या r है। (I घिरनी का जड़त्व आघूर्ण) ब्लॉक का त्वरण तथा घिरनी का कोणीय त्वरण ज्ञात कीजिए |

View SolutionFind the acceleration of center of mass of the blocks of masses m_(1) and m_(2) (m_(1)gtm_(2)) in Atwood.s machine:
View Solution
