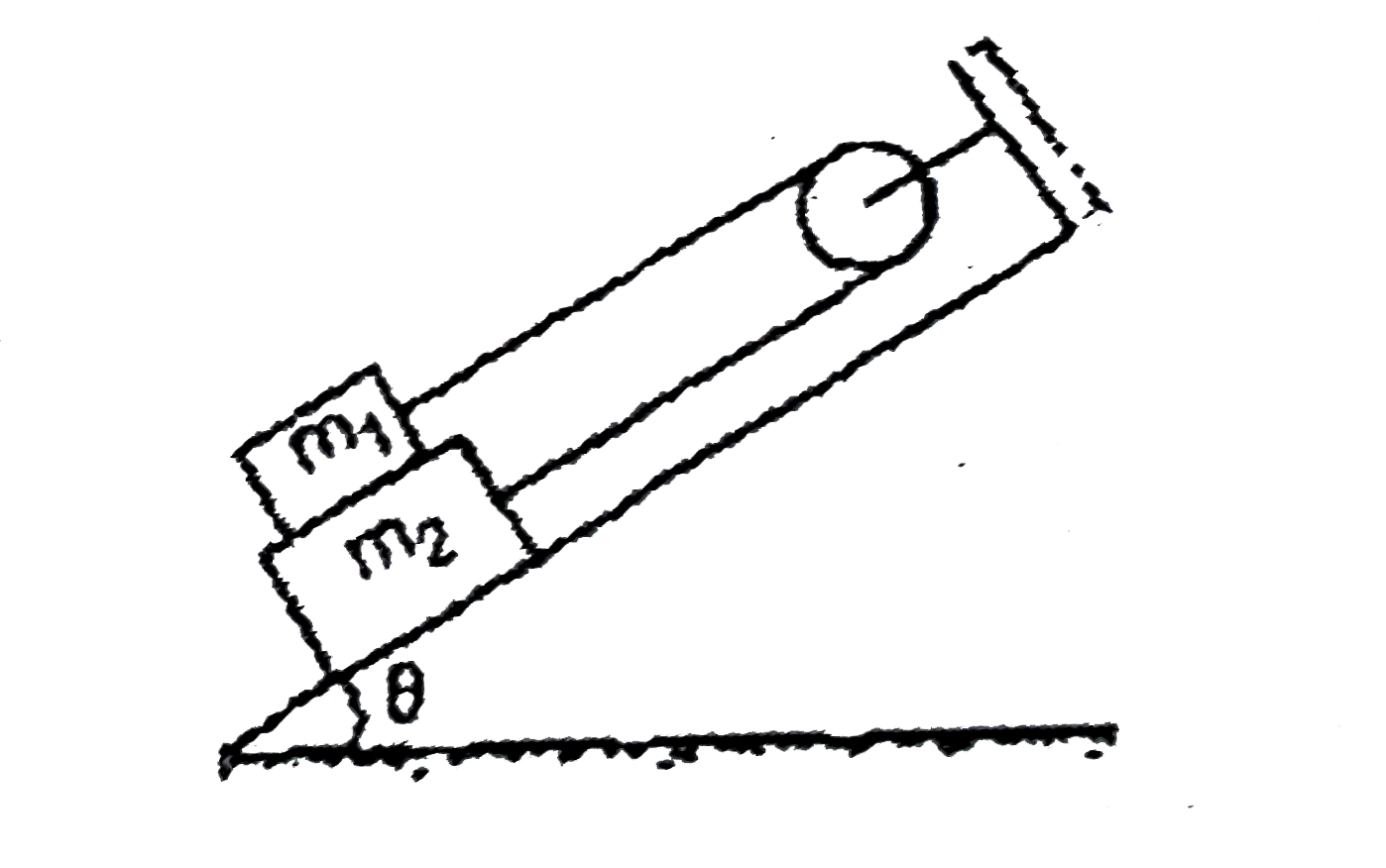
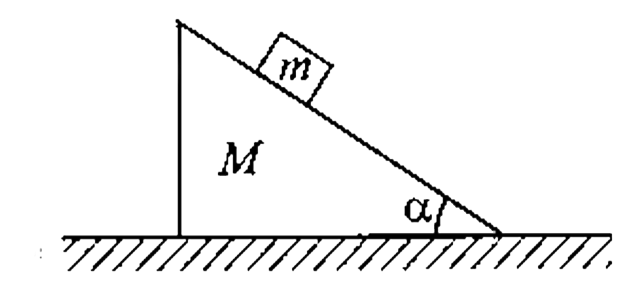
Figure shows a block of mass m1 sliding on a block of mass m2, with m1>m2. Find the

(a) acceleration of each block
(b) tension in the string
(c ) force exerted by m1 on m2. ltbr> (d) force exerted by m2 on the incline.
The correct Answer is:(a) a=m1gsinθ−m2gsinθm1+m2 (b) 2m1m2gsinθm1+m2 (c ) m1gcosθ (d) (m1gcosθ+m2gcosθ)
Figure shows free body diagram of each block. We will apply Newton's second law along x- and y-axis shown in free body diagram. Block m1 is heavy, hence it slides down whereas m2 slides up.
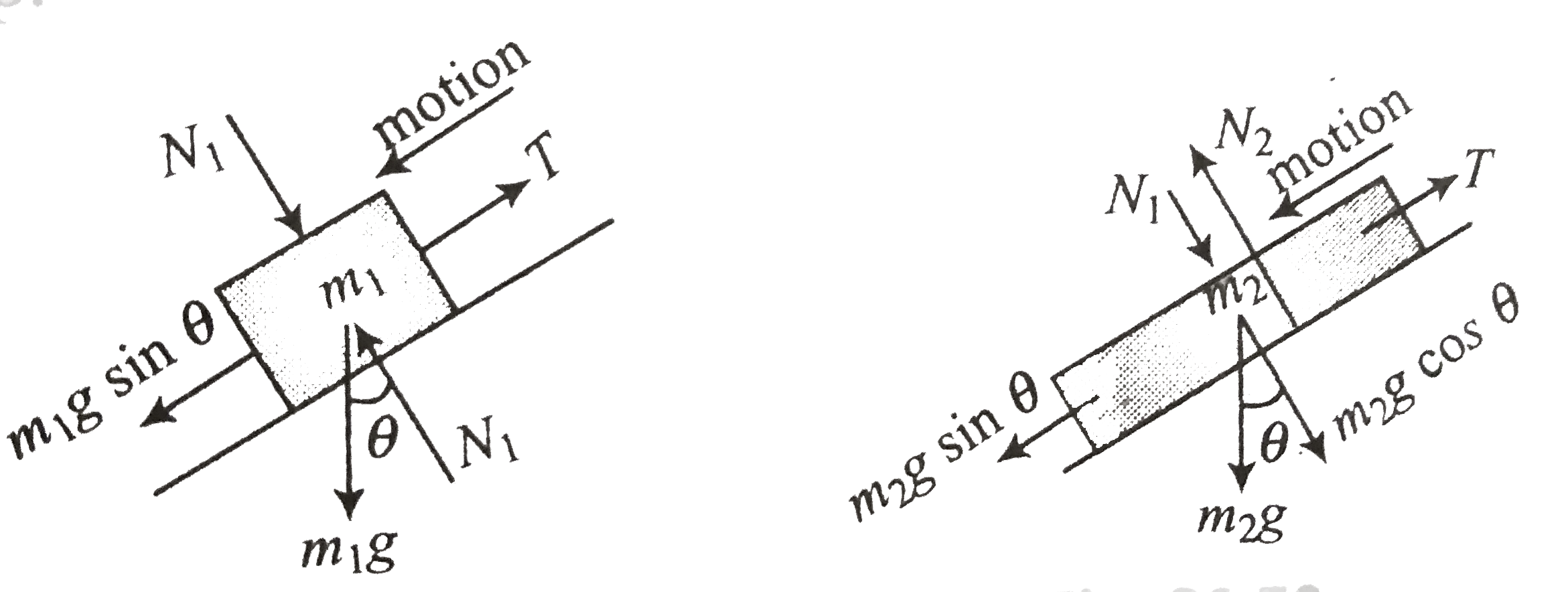
ΣFx=m1gsinθ−T=m1a
ΣFy=N1−m1gcosθ=0
ΣFx=T−m2gsinθ=m2a
ΣFy=N2−N1−m2gcosθ=0
From eq. (i) and (iii),
a=m1gsinθ−m2gsinθm1+m2
T=m2a+m2gsinθ
=m2(m1gsinθ−m2sinθ)m1+m2+m2gsinθ
=2m1m2gsinθm1+m2
From Eqs. (ii) and (iv)
N1=m1gcosθ
N2=N1+m2gcosθ=(m1gcosθ−m2gcosθ)
N1 is force exerted by block m1onm2andN2 is force exerted by block m2 on inclined surface.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct
76 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
(a) shows a block of mass m1 sliding on a block of mass m2, with m1>m2. Find
(a) the acceleration of each block,
(b) tension in the string,
(c) force exerted by m1 on m2
(d) force exerted by m2 on the incline
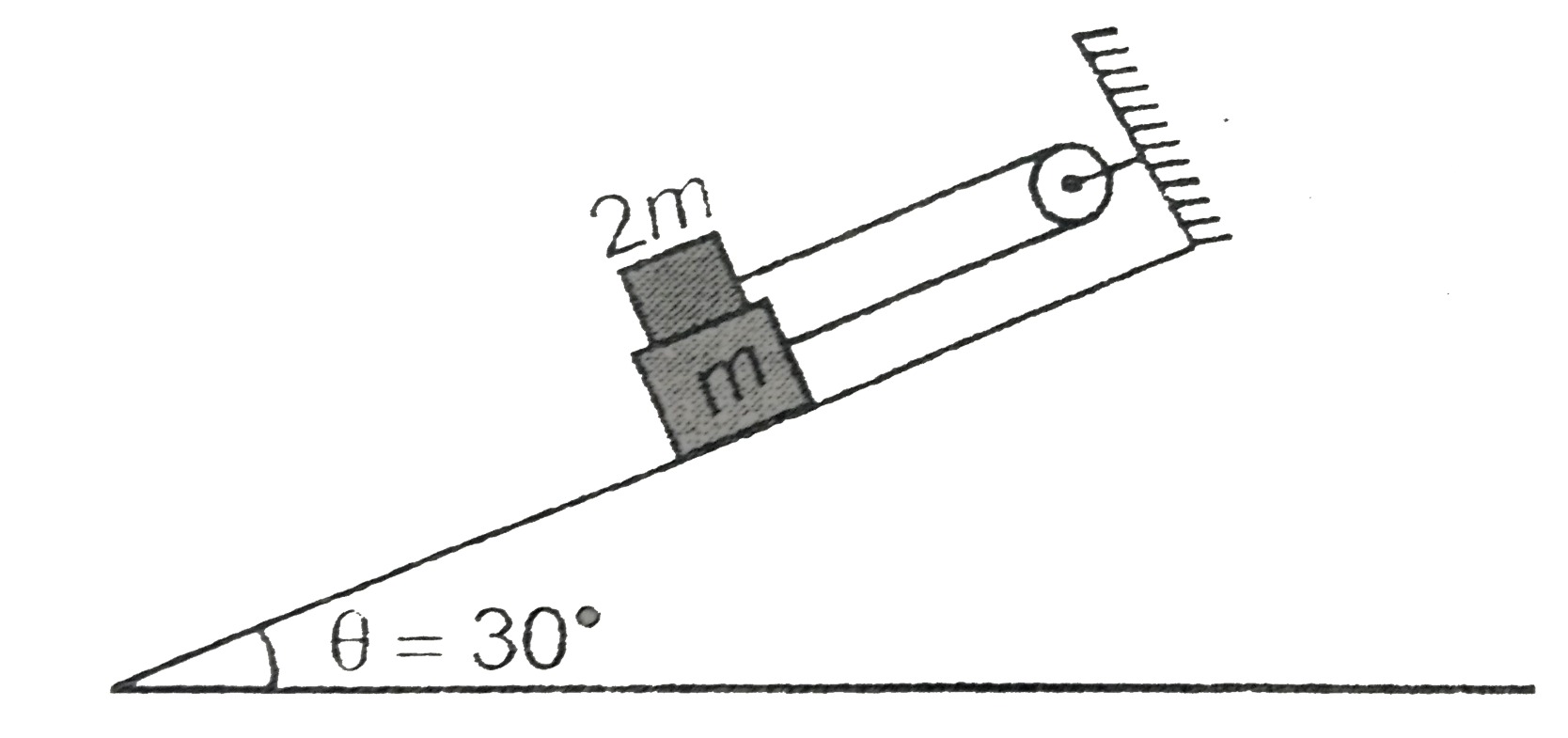
View SolutionFigure shows a block of mass 2m sliding on a block of mass m. Find the acceleration of each block . ( All surface are smooth )
View Solution
Knowledge Check
Two block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
 Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2A body A mass m1 exerts a force on another body B of mass m2 . If the acceleration of B be a2 , then the acceleration (in magnitude) of A is
Am2m1a2Bm1m2a2Cm1m2a2D(m1+m2)a2
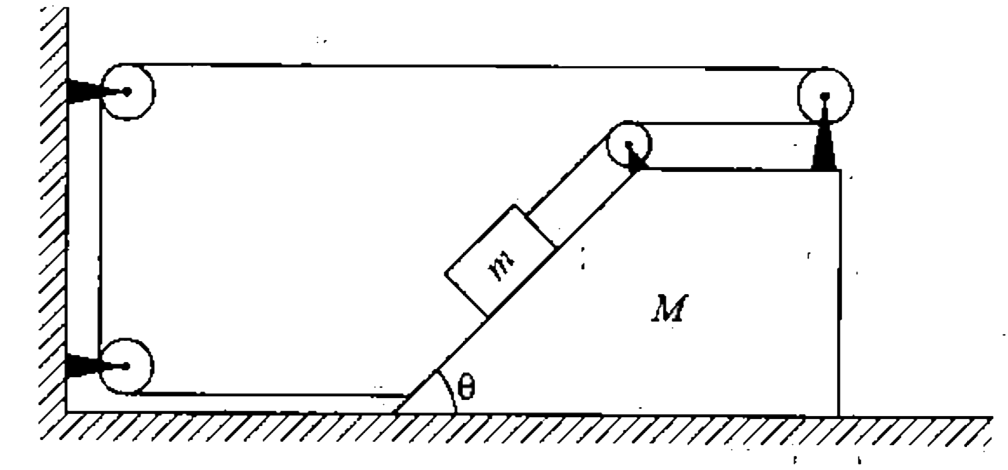
Figure-2.64 shows a block of mass M supporting a bar of mass m through a pulley system. If system is released from rest, find the acceleration of block M and the tension in the strings
View SolutionFigure shows a pulley of mass m and radius r with two blocks of masses m1 and m2 attached with a light and unstretchable string. Find the acceleration of the blocks, tensions in the string and the force exerted by the pulley on the celling from which it is hanging. Assume no slipping between the string and the wheel.
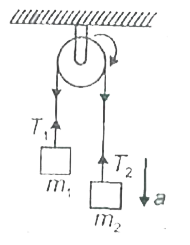
View SolutionFind the acceleration of each block in the figure shown below, in terms of their masses m1,m2 and g. Neglect any friction.

View SolutionFigure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
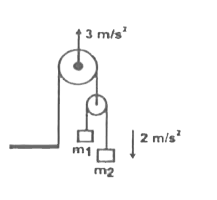
View SolutionIn the figure shown, the acceleration of block of mass m2 is 2m/s2. The acceleration of m1 :
View Solution
