In fig. the man and the platform together weight 950N. The pulley can be treated as frictionless. Determine how hard the man has to pull on the rope to lift himself upward above the ground with constant velocity. If the weight of man is 550 N, what is the normal reaction between them?

The correct Answer is:20 kg wt; 40 kg wt; 80 kg wt.
Let N be the reaction between man and platform. T1 is the tension in string passing over pulley 1, T2 is the tension in string passing over pulley 2. M is the mass of man, m is the mass of platform.
The free-body diagram of man platform and pulley 2 are shown in fig.
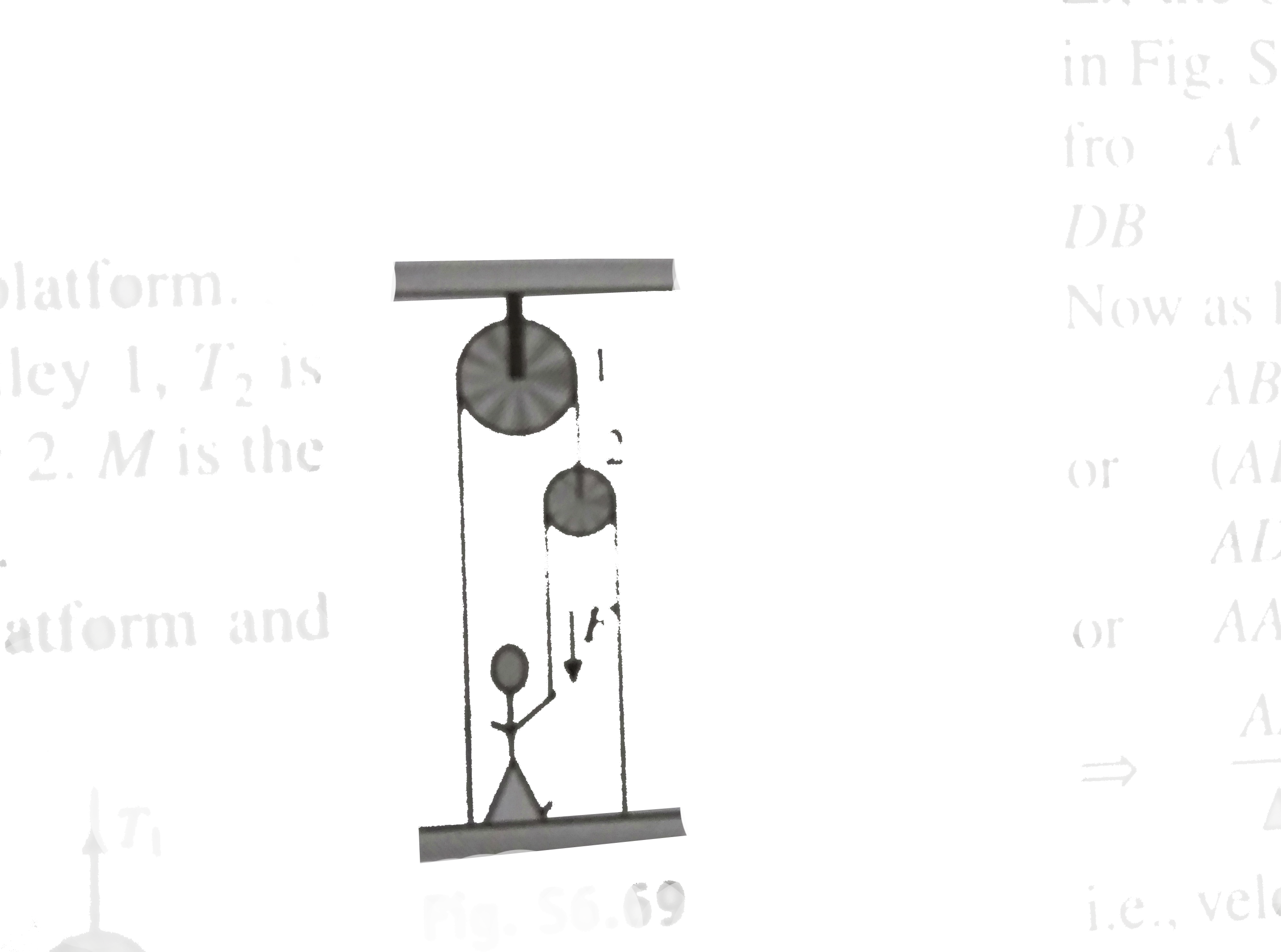
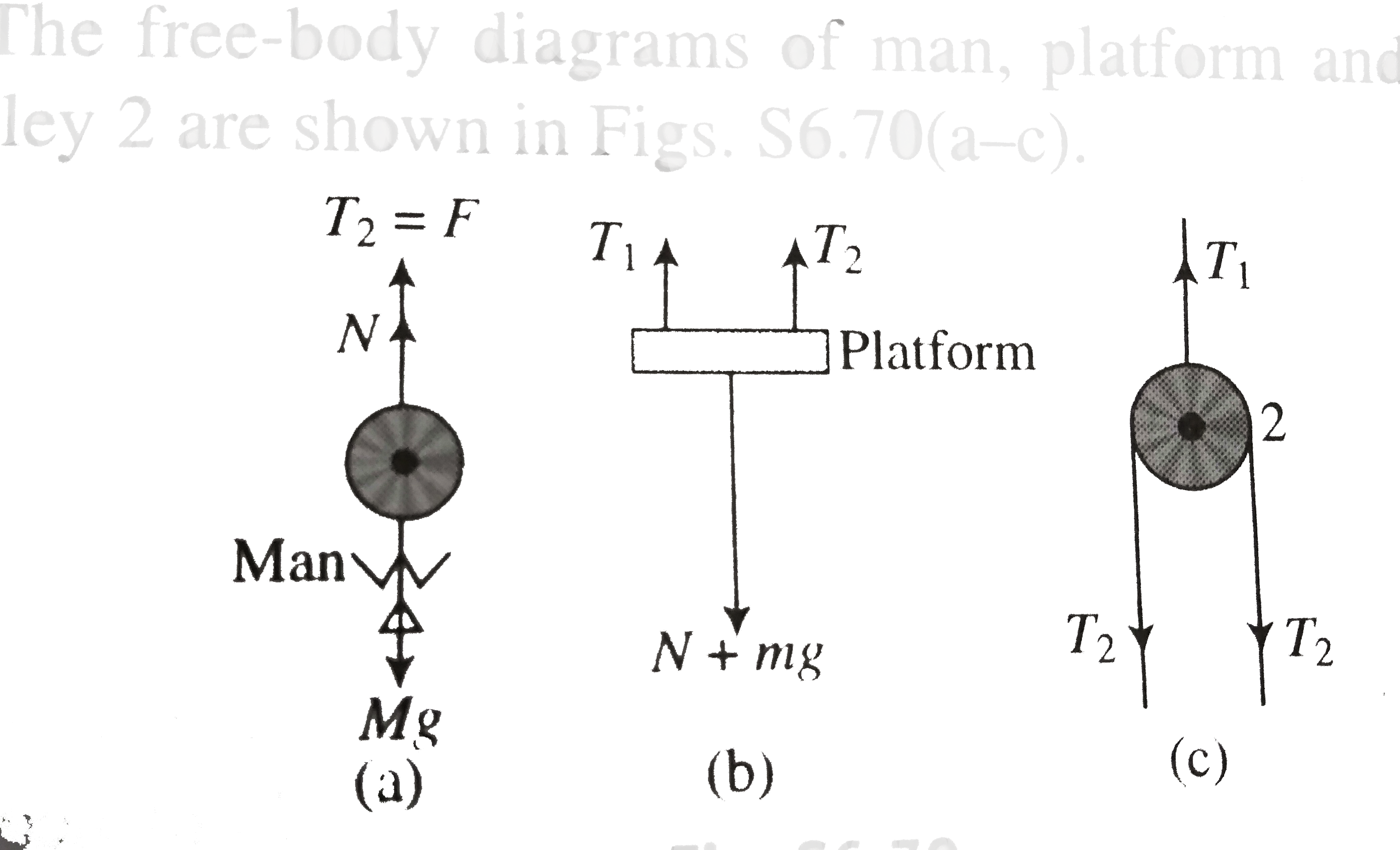
Action exerted by man of platfrom =reaction exerted by platform on man =N
For equilibrium of man: Mg=T2+N ..(i)
For equilibrium of platform: T1+T2=M+Mg ...(ii)
For equilibrium of pulley 2, T1=2T2 ...(iii)
Adding Eqs. (iii) we get
T1+T2+(T2+N)=N+mg+Mg
T1+2T2=(M+m)g
Using Eq. (iii), we get 2T2+2T2=(M+m)g
⇒T2=(M+m)4g
∴F=T2=(M+m)4g=(60+204)gN=20kgwt.
Now From eq (i)
N=Mg−T2=Mg−F=Mg−(M+m)4g1
=(3M−m)4g ...(v)
=(3×60−204)g=40kgwt
Form Eq. (v), mg=3Mg−4N
Clearly mg is maximum when N is minimum.
Minimum N=0
so, (mg)max=3Mg=3×60g=180kgwt.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Single Correct
76 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
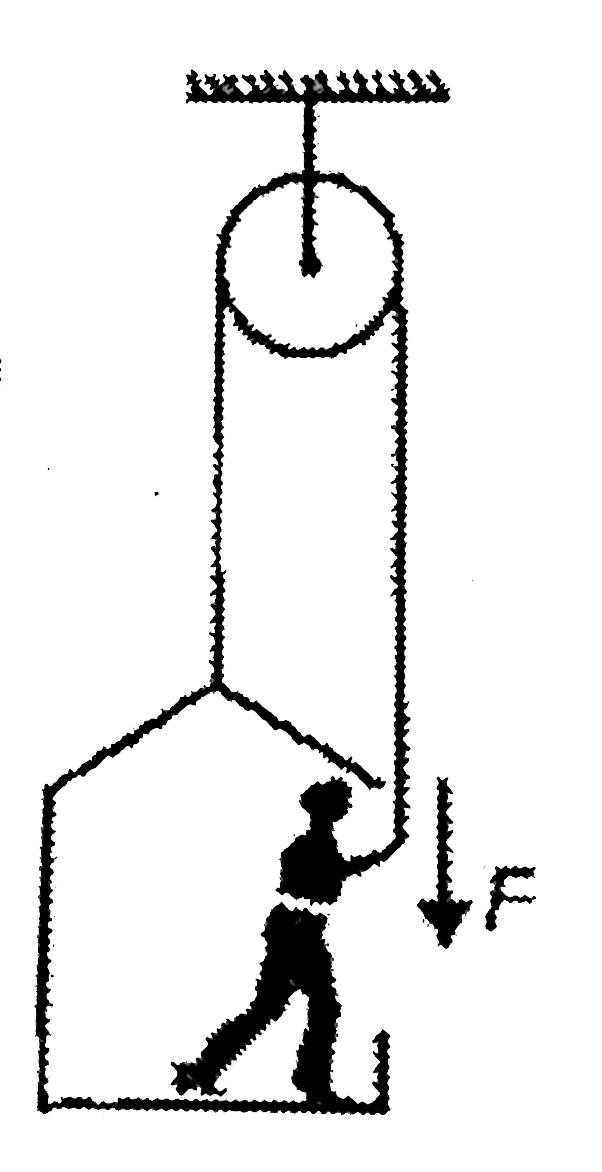
A man of mass M stands on a.box of mass m as shown in the Fig. 2E. l (a). A rope attached to 'the box and passing over an overhead pulley allows the man to raise himself and the box by , pulling the rope downward.
(i) With what minimum force should the ' man pull the rope so as to prevent himself , from falling down.
(ii) If the man pulls the rope with a force F greater than the minimum force, then determine the acceleration of the (man + box) system.
(iii) Determine. the normal reaction between the man and the trolley.
View SolutionA man with mass 85 kg stands on a platform with mass 25 kg. He pulls on the free end of a rope that runs over a pulley on the ceiling and has its other end fastened to the platform. The mass of the rope and the mass of the pulley can be neglected, and the pulley is frictionless. With what force does he have to pull so that he and the platform have an upward acceleration of 2.2ms2. (Take g=10ms2)
View Solution
Knowledge Check
A uniform ladder 5.0m long rests against a frictionless, vertical wall with its lower end 3.0m to from the wall. The ladder weighs 160N. The coefficient of static friction between the foot of the ladder and the ground is 0.40. A man weighing 740N climbs slowly up the ladder.
What is the actual frictional force when the man has climbed 1.0m along the ladder?A360NB171NC900ND740NA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If a clown holds on to hoop instead of passing through it, what is the position of the cable so that he doesn't hit his head on the ceiling as he swings upward?A2v20gBv20gCv202gDv204gA man stands on a rotating platform with his arms stretched holding a 5kg weight in each hand. The angular speed of the platform is 1.2revs−1. The moment of inertia of the man together with the platform may be taken to be constant and equal to 6kgm2. If the man brings his arms close to his chest with the distance n each weight from the axis changing from 100cm to20cm. The new angular speed of the platform is.
A2revs−1B3revs−1C5revs−1D6revs−1
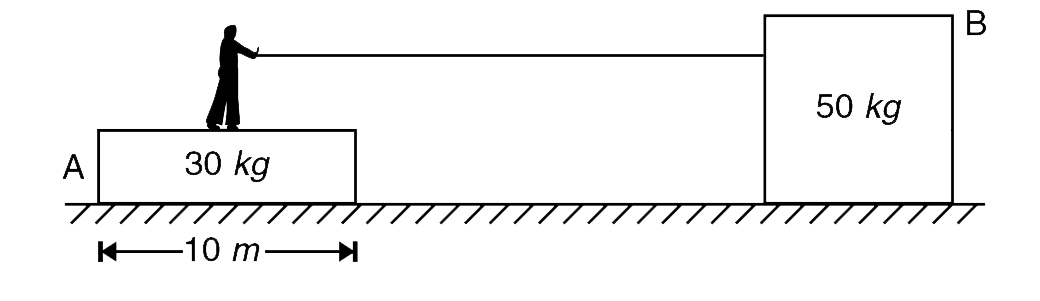
A 50 kg man is standing at the centre of a 30 kg platform A. Length of the platform is 10 m and coefficient of friction between the platform and the horizontal ground is 0.2. Man is holding one end of a light rope which is connected to a 50 kg box B. The coefficient of friction between the box and the ground is 0.5. The man pulls the rope so as to slowly move the box and ensuring that he himself does not move relative to the ground. If the shoes of the man does not slip on the platform, calculate how much time it will take for the man to fall off the platform. Assume that rope remains horizontal, and coefficient of friction between shoes and the platform is 0.6.
View SolutionBlocks A,BandC are placed as shown in Fig and connected by the rops of negligible mass . Both A and B weigh 25.0N each , and the coefficient of kinetic friction between each and the surface is 0.35 blocks C descends with constant velocity .

a. Draw two separate free- body diagrams showing the forces acting on AandB
b. Find the tension in the rope connecting blocks AandB
c. What is the weight of blocks C?
d. If the rope connecting AandB were cut, what would be the acceleration of C?
View SolutionFigure 5-55 shows a man sitting in a bosun's chair that dangles from a mass-less rope, which runs over a massless, frictionless pulley and back down to the man's hand. The combined mass of man and chair is 103.0 kg. With what force magnitude must the man pull on the rope if he is to rise (a) with a constant velocity and (b) with an upward acceleration of 1.30 m/s2 ?
View SolutionSuppose that a man (60 kg) is standing in an elevator. The elevator accelerates upward from rest at 1m/s2 for 2 sec then for further 10 sec it moves with the constant velocity and then decelerates at the same rate for 2 sec
(a) For the whole motion, how much work is done by the normal force on the man by the elevator floor?
(b) By man's weight
(c) what average power is delivered by the normal force for the whole motion
(d) What instantaneous power is delivered by the normal force at 7 sec ?
(e) at 13 sec ?
View SolutionA rope is stretched between two stationary boats on the surface of a lake. A man in the first boat pulls the rope with a constant force of 100 N. The distance between the boats is 100 m in the beginning. The mass of the first boat with the man is 250 kg ,while the mass of the other is 500 kg. Find :(i) the velocity of approach of the two boats 15 s after the start,(ii) the time taken for the two boats to meet each other. [Hint: Consider relative acceleration and apply kinematic equations.]
View Solution
