A mass m is released from the top of a vertical circular track of radius r with a horizontal speed v0. Calculate the angle θ with respect o the vertical where it leaves contact with the track. Solution in Telugu
The forces acting on the body are its weight mg and reaction N as shown in Fig.
So for circular motion of the body at any posiotion θ

mv2r=mgcosθ−N or
N=mgcosθ−mv2r
The body will leave contact where N = 0
i.e., mgcosθ=mv2r=0 i.e., cosθ=v2rg .....(2)
Now applying conservation of mechanical energy between H and P, we get
12mv2=12mv20+mgr(1−cosθ)
where .v. is the velocity at .P.
[as y=r(1−cosθ)]
or v2=v20+2gr(1−cosθ) ......(3)
substituting the value of v2 in Equation (2)
cosθ=v20rg+2(1−cosθ)
i.e., cosθ=[v203rg+23]orθ=cos−1[v203rg+23]
Topper's Solved these Questions
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 1A
117 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 1B
39 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
36 Videos
- WORK, POWER & ENERGY BOOK - AAKASH SERIESCHAPTER - WORK, POWER & ENERGY EXERCISE - PRACTICE EXERCISE (PERFECTLY INELASTIC COLLISIONS)
5 Videos
Similar Questions
If l1,m1,n1 and l2,m2,n2 are the direction cosines of two vectors and θ is the angle between them, then the value of cos θ is
View Solution(A): A spring has potential energy, both when it is compressed or stretched.
(R) : In compressing or stretching, work is done on the spring against the restoring force.
View SolutionThe velocity of a particle of mass 10−2kg is given as →v=(2xˆu+3yˆj+4zˆk) m/sec (where x, y and z are in meter). The amount of work done by applied force in displacing a particle from (1m, 2m, 0) to (-1m, 3m, 1m) is …..
View SolutionA shot moving with a velocity 140ms−1 collides a wooden block and comes to rest in it. If mass of the block is 13 times the mass of the shot, velocity of the block is
View SolutionA section of fixed smooth circular track of radius R in vertical plane is shown in the figure. A block id released from position A and leaves the treack at B The radius of curvanture of its trajectory just after it leaves the track B is ?
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionIn the figure shown, a small ball of mass 'm' can move witgout sliding in a fixed semicircular track of radius R in vertical planet. It is released from the top. The resultant force on the ball at the lowest of the track is
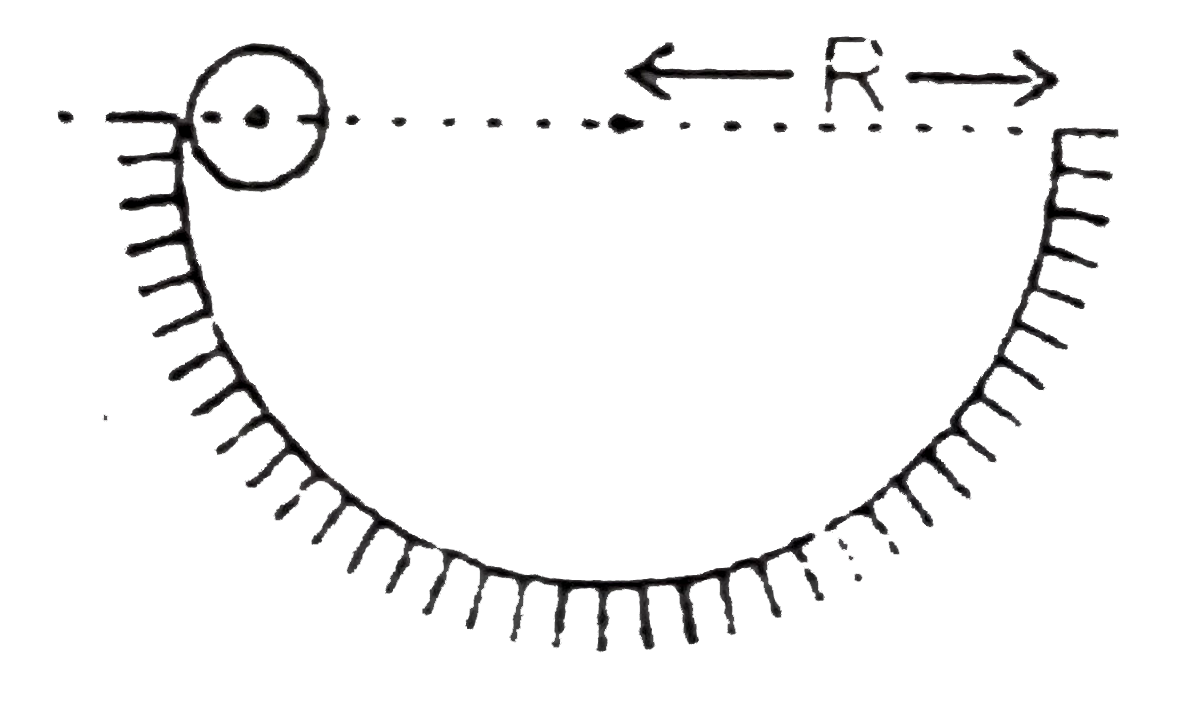
View SolutionIn a circus stuntman rides a motorbike in a circular track of radius R in the vertical plane. The minimum speed at highest point of track will be
View SolutionAs shown in the figure, a small is released from a certain height h which has to perform circular motion on a vertical smooth track of radius 4 m. the track is absent between point A and B. Calculate the height (in m) from where the ball has to be released so that it will reach at highest point B of the circular track
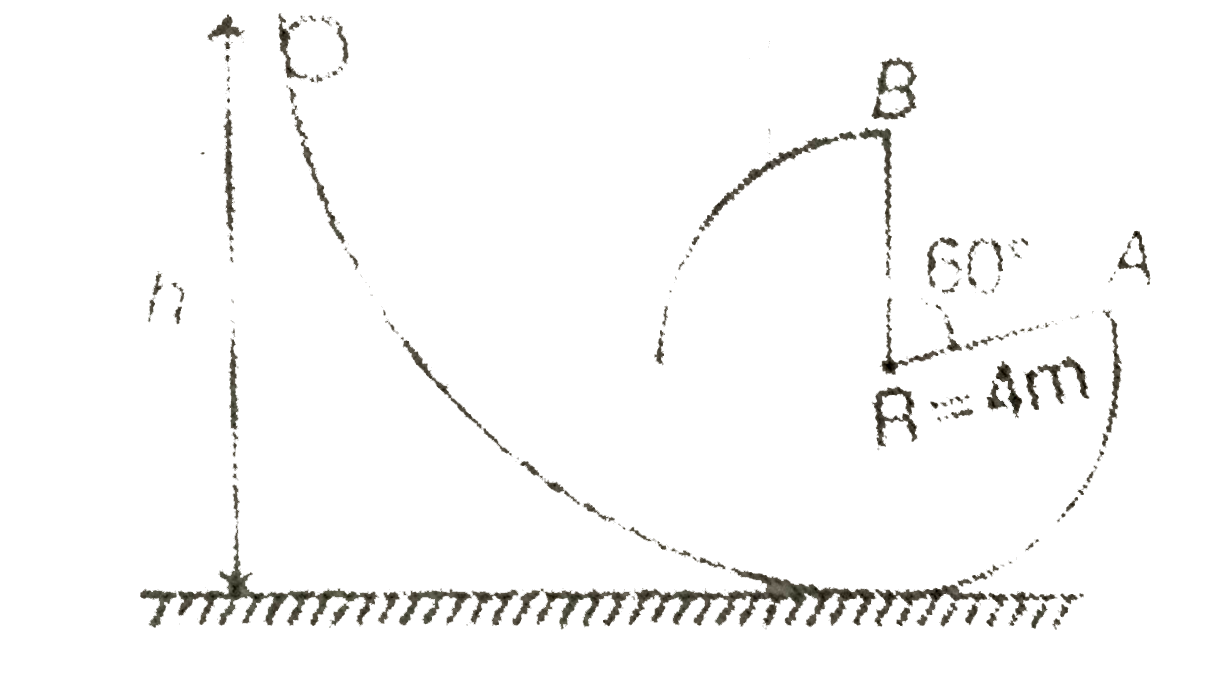
View SolutionIn a circus , stuntman rides a motor bike in a circular track of radius R in the vertical plane. The minimum speed at highest point of track will be _______ .
View SolutionAn inclined track ends in a circular loop of radius 'r'. From what height on the track a particle should be released so that it completes that loop in the vertical plane?
View SolutionA mass m is released with a horizontal speed v from the top of a smooth and fixed, hemispherical bowl, of radius r. The angle theta w.r.t the vertical where it leaves contact with the bowl is
View SolutionA mass .m. is released, with a horizontal speed v from the top of a smooth and fixed, hemispherical bowl, of radius r. The angle theta w.r.t. the vertical where it leaves constant with the bowl is
View SolutionA mass.m. is released, with a horizontal speed v from the top of a smooth and fixed, hemispherical bowl, of radius r. The angle theta w.r.t. the vertical where it leaves contact with the bowl is
View SolutionA mass m is released from the top of a vertical circular track of radius r with a horizontal speed v_(theta) . Calculate the angle theta with respect to the vertical where it leaves contact with the track.
View Solution
