Find the areas enclosed between the circle x2+y2−2x+4y−11=0 and the parabola y=−x2+2x+1−2√3
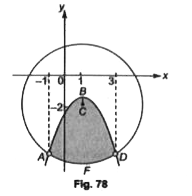
The correct Answer is:323−4√3+83π
Related Playlists
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Areas with Parametrically Represented Boundaries7videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - The Area of a Curvilinear Sector in Polar Coordinates5videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Finding Average Values of a Function15videos
APPLICATIONS OF THE DEFINITE INTEGRAL
- BOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS9videos
APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONS
- BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS5videos
BASIC CLASSES OF INTEGRABLE FUNCTIONS
Similar Questions
find the area enclosed between the curves y=x2−5x and y=4−2x
View SolutionFind the area enclosed between the curves
y2=2x,y=4x−1View SolutionWhat is the difference between 2.0m and 2.00m.
View SolutionFind the area lying above x-axis and included between the circle x2+y2=8xand the parabola y2=4x.
View SolutionFind the area, lying above the x=axis and included between the circle x2+y2=8x and the parabola y2=4x.
View SolutionFind the area enclosed between circle x2+y2=1 and the line x+y=1 in first quadrant.
View SolutionFind the area enclosed by circle x2+y2=4 ,parabola y=x2+x+1 , the curve y=[∣∣∣sin2x4+cosx4∣∣∣] and x-axis
View SolutionFind the area, lying above the x-axis and included between the circle x2+y2=8x and the parabola y2=4x.
View SolutionFind the area of the region enclosed between the two circles x2+y2=1 and (x−1)2+y2=1
View SolutionFind the area of the region enclosed between the two circles x2+y2=1 and (x−1)2+y2=1
View Solution

