Find the area, lying above the x=axis and included between the circle $x^{2} + y^{2} = 8 x$ and the parabola $y^{2} = 4 x .$

Video Solution

Text Solution

Verified by Experts

Solving the curves, we get $x^{2} + 4 x = 8 x \Rightarrow x = 0, 4$

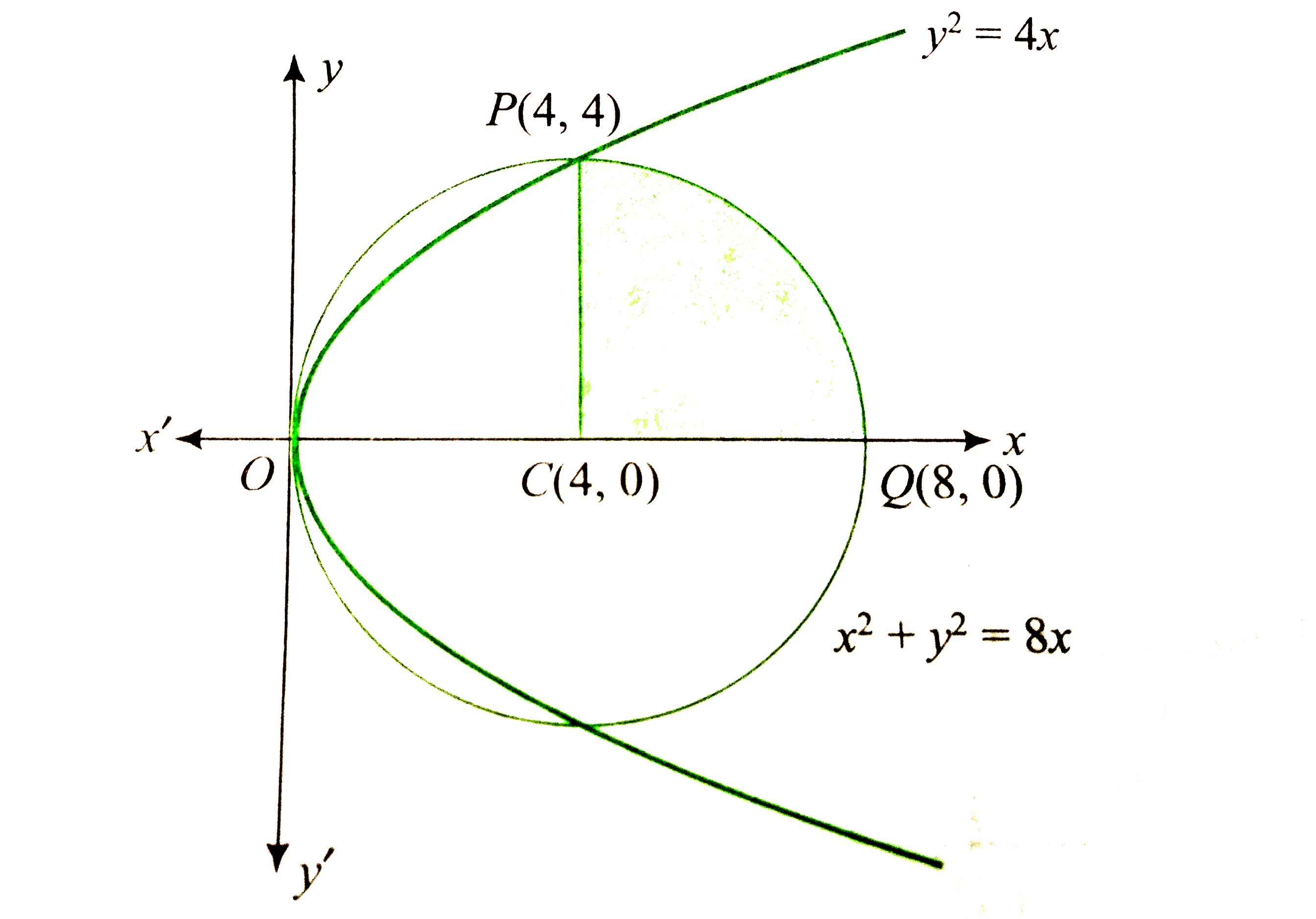
$Required area = \int_{0}^{4}^{y} parabola d x + \int_{4}^{8}^{y} circle d x$
$Circle is {(x - 4)}^{4} + y^{2} = 4^{2},$
$Area of quarter of circle = \frac{1}{4} π 4^{2} = 4 π$
$= \int_{0}^{4} 2 \sqrt{x} d x + 4 π$
$= \frac{4}{3} {[x^{3 / 2}]}_{0}^{3 / 2} + 4 π$
$= \frac{4}{3} \times 4 \sqrt{4} + 4 π sq. units$
$= \frac{32}{3} + 4 π sq. units$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the region lying above x - axis, and included between the circle $x^{2} + y^{2} = 2 a x$ & the parabola $y^{2} = a x, a > 0$ is
A $8 π a^{2}$
B $a^{2} (\frac{π}{4} - \frac{2}{3})$
C $\frac{16 π a^{2}}{9}$
D $π (\frac{27}{8} + 3 a^{2})$
Question 2 - Select One
Area above the X-axis, bounded by the circle $x^{2} + y^{2} - 2 a x = 0$ and the parabola $y^{2} = a x$ is
A $a^{2} (\frac{π}{4} - \frac{2}{3})$
B $a^{2} (\frac{π}{4} + \frac{2}{3})$
C $2 a^{2} (\frac{π}{4} + \frac{2}{3})$
DNone of these

Recommended Questions

Home
Ask Doubt
Profile