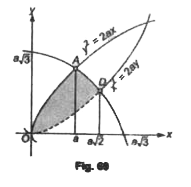
Compute the area of the figure which lies in the first quadrant inside

Area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ the line $x = \sqrt{3} y$ and x-axis , is
A $π$
B $π / 2$
C $π / 3$
DNone of these
If the circle $x^{2} + y^{2} + 2 a x = 0, a \in R$ touches the parabola $y^{2} = 4 x$ , them
A $a \in (- \infty, 0)$
B $a \in (0, \infty)$
C $a \in (2, \infty)$
Dnone of these
Area lying in the first quadrant and bounded by the circle $x^{2} + y^{2} = 4$ and the lines $x = 0 and x = 2$ is :
A $π$
B $\frac{π}{2}$
C $\frac{π}{2}$
D $\frac{π}{4}$

Compute the area of the figure which lies in the first quadrant inside the circle $x^{2} + y^{2} = 3 a^{2}$ and is bounded by the parabolas $x^{2} = 2 a y and y^{2} = a x (a > 0)$