Let [x] be the greatest integer less than or equal to x, for a real number x. Then the equation [x2]=x+1 has
two solutions
one solution
no solution
more than two solutions
To solve the equation (x2)=x+1, where (x) denotes the greatest integer less than or equal to x, we can follow these steps:
Step 1: Understand the equation
The equation states that the greatest integer less than or equal to x2 is equal to x+1. This implies that x+1 must be an integer, which means x must be of the form n−1 for some integer n.
Step 2: Set up the inequality
From the definition of the greatest integer function, we can express this as:
n−1≤x<n
This leads to:
n−1≤x<n⟹n−1≤x<n
Now substituting x+1=n into the equation gives:
(x2)=n
Step 3: Analyze the equation
This means:
n≤x2<n+1
Substituting n=x+1 gives:
x+1≤x2<x+2
Step 4: Solve the inequalities
We can break this down into two inequalities:
1. x+1≤x2
2. x2<x+2
Solving the first inequality:
x2−x−1≥0
To find the roots, we use the quadratic formula:
x=−(−1)±√(−1)2−4⋅1⋅(−1)2⋅1=1±√52
The roots are:
x1=1+√52,x2=1−√52
The inequality x2−x−1≥0 holds for x≤x2 or x≥x1.
Solving the second inequality:
x2−x−2<0
Finding the roots:
x=−(−1)±√(−1)2−4⋅1⋅(−2)2⋅1=1±√92=1±32
The roots are:
x3=2,x4=−1
The inequality x2−x−2<0 holds for −1<x<2.
Step 5: Combine the intervals
Now we combine the intervals from both inequalities:
1. From x2−x−1≥0: x≤1−√52 or x≥1+√52.
2. From x2−x−2<0: −1<x<2.
The only feasible solution occurs in the interval:
(−1,2)∩(−∞,1−√52)∪(1+√52,∞)
However, since 1+√52≈1.618, the only valid interval is:
(1+√52,2)
Conclusion
Since there are no integer solutions that satisfy both inequalities simultaneously, we conclude that the equation (x2)=x+1 has no solutions.
The equation states that the greatest integer less than or equal to x2 is equal to x+1. This implies that x+1 must be an integer, which means x must be of the form n−1 for some integer n.
From the definition of the greatest integer function, we can express this as:
n−1≤x<n
This leads to:
n−1≤x<n⟹n−1≤x<n
Now substituting x+1=n into the equation gives:
(x2)=n
This means:
n≤x2<n+1
Substituting n=x+1 gives:
x+1≤x2<x+2
We can break this down into two inequalities:
1. x+1≤x2
2. x2<x+2
x2−x−1≥0
To find the roots, we use the quadratic formula:
x=−(−1)±√(−1)2−4⋅1⋅(−1)2⋅1=1±√52
The roots are:
x1=1+√52,x2=1−√52
The inequality x2−x−1≥0 holds for x≤x2 or x≥x1.
x2−x−2<0
Finding the roots:
x=−(−1)±√(−1)2−4⋅1⋅(−2)2⋅1=1±√92=1±32
The roots are:
x3=2,x4=−1
The inequality x2−x−2<0 holds for −1<x<2.
Now we combine the intervals from both inequalities:
1. From x2−x−1≥0: x≤1−√52 or x≥1+√52.
2. From x2−x−2<0: −1<x<2.
(−1,2)∩(−∞,1−√52)∪(1+√52,∞)
However, since 1+√52≈1.618, the only valid interval is:
(1+√52,2)
Since there are no integer solutions that satisfy both inequalities simultaneously, we conclude that the equation (x2)=x+1 has no solutions.
Topper's Solved these Questions
- KVPY 2021Book:KVPY PREVIOUS YEARChapter:KVPY 2021Exercise:PART I (Chemistry)
Explore 2 Videos
- KVPY 2021Book:KVPY PREVIOUS YEARChapter:KVPY 2021Exercise:PART-I Mathematics
Explore 19 Videos
- KVPYBook:KVPY PREVIOUS YEARChapter:KVPYExercise:exercise
Explore 18 Videos
- MOCK TEST 1Book:KVPY PREVIOUS YEARChapter:MOCK TEST 1Exercise:EXERCISE
Explore 26 Videos
Similar Questions
Knowledge Check
Let [x] be the greatest integer less than or equal to x, for a real number x. Then the following sum
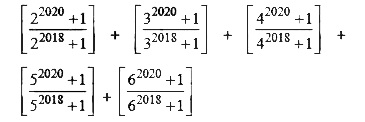
is-A80B85C90D95Let [x] denote the greatest integer less than or equal to x for any real number x. then limx→∞[n√2]n is equal to
A0B2C√2D1If [x] denotes the greatest integer less than or equal to x, then the solutions of the equation 2x-2[x]=1 are
Ax=n+12,n∈NBx=n−12,n∈NCx=n+12,n∈NDn<x<n+1,n∈Z
Let [x] denote the greatest integer less than or equal to x. Then, ∫−11[x]dx=?
View SolutionLet [x] denote the greatest integer less than or equal to x. Then, ∫1.50[x]dx=?
View SolutionIf [x] denotes the greatest integer less than or equal to x for any real number x. Then, limx→∞[n√2]n is
View SolutionLet [x] denotes the greatest integer less than or equal to x if x=(√3+1)5then [x] is equal to
View SolutionLet [x] denotes the greatest integer less than or equal to x. If f(x)=[xsinπx], then f(x) is
View Solution