Let a = BC, b = CA, c = AB be side lengths of a triangle ABC. And m be the length of the median through A. If a = 8, b-c = 2, m = 6, then the nearest integer to b is
7
8
9
10
To solve the problem, we will use the given information about the triangle ABC and the formula for the length of the median.
1. Identify the given values:
- a=BC=8
- b−c=2 (which means b=c+2)
- m=6 (length of the median from A)
2. Use the formula for the length of the median:
The formula for the length of the median m from vertex A to side BC is given by:
m=12√2b2+2c2−a2
Plugging in the known values:
6=12√2b2+2c2−82
3. Simplify the equation:
First, multiply both sides by 2:
12=√2b2+2c2−64
Now, square both sides:
144=2b2+2c2−64
Rearranging gives:
2b2+2c2=208
Dividing everything by 2:
b2+c2=104
4. Substitute b in terms of c:
Since b=c+2, substitute this into the equation:
(c+2)2+c2=104
Expanding the left side:
c2+4c+4+c2=104
Combine like terms:
2c2+4c+4=104
Rearranging gives:
2c2+4c−100=0
Dividing the entire equation by 2:
c2+2c−50=0
5. Solve the quadratic equation:
Using the quadratic formula c=−b±√b2−4ac2a:
Here, a=1,b=2,c=−50:
c=−2±√22−4⋅1⋅(−50)2⋅1
c=−2±√4+2002
c=−2±√2042
c=−2±2√512
c=−1±√51
Since c must be positive, we take:
c=−1+√51
6. Find b:
Now substitute back to find b:
b=c+2=(−1+√51)+2=1+√51
7. Approximate b:
We know √51 is approximately 7.14, so:
b≈1+7.14=8.14
8. Find the nearest integer to b:
The nearest integer to 8.14 is 8.
Final Answer
The nearest integer to b is 8.
- a=BC=8
- b−c=2 (which means b=c+2)
- m=6 (length of the median from A)
The formula for the length of the median m from vertex A to side BC is given by:
m=12√2b2+2c2−a2
Plugging in the known values:
6=12√2b2+2c2−82
First, multiply both sides by 2:
12=√2b2+2c2−64
Now, square both sides:
144=2b2+2c2−64
Rearranging gives:
2b2+2c2=208
Dividing everything by 2:
b2+c2=104
Since b=c+2, substitute this into the equation:
(c+2)2+c2=104
Expanding the left side:
c2+4c+4+c2=104
Combine like terms:
2c2+4c+4=104
Rearranging gives:
2c2+4c−100=0
Dividing the entire equation by 2:
c2+2c−50=0
Using the quadratic formula c=−b±√b2−4ac2a:
Here, a=1,b=2,c=−50:
c=−2±√22−4⋅1⋅(−50)2⋅1
c=−2±√4+2002
c=−2±√2042
c=−2±2√512
c=−1±√51
Since c must be positive, we take:
c=−1+√51
Now substitute back to find b:
b=c+2=(−1+√51)+2=1+√51
We know √51 is approximately 7.14, so:
b≈1+7.14=8.14
The nearest integer to 8.14 is 8.
The nearest integer to b is 8.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let a = BC, b = CA, c = AB be side lengths of a triangle ABC. And m be the length of the median through A. If a = 8, b-c = 2, m = 6, then the nearest integer to b is
A7B8C9D10Let a, b, c be the side-lengths of a triangle, and l, m,n be the lengths of its medians. Put K=(l+m+na+b+c) Then, as a, b, c vary, K can assume every value in the interval
A(14,45)B(12,45)C(34,1)D(45,54)The sides of a triangle ABC are 6, 7, 8, the smallest angle being C then
The length of the median from C isA√951B√952C√953Dnone
In a triangle ABC the length of the sides, AB is 3 m and BC is 5 m what is the length of AC, if the angle formed at B is 60∘
View SolutionLet →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
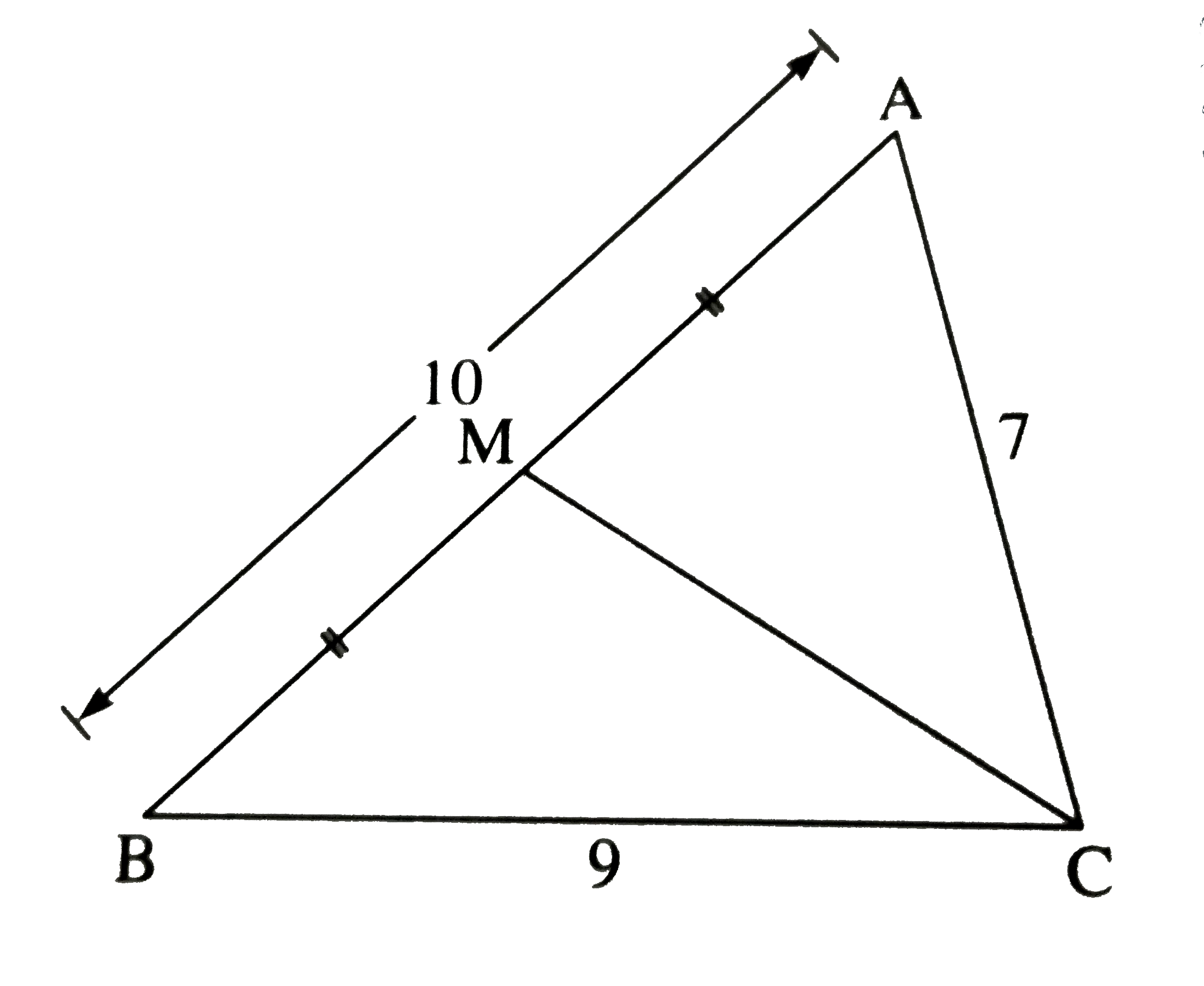
View SolutionIn △ABC , AB=10
AC=7,BC=9
then find the length find the length of the median drawn from point C to side AB .
View SolutionVertices of a ΔABC are A(2, 2), B (-4, -4) and C (5, -8) , then the length of the median through C is
View SolutionVertices of a ΔABC are A(2, 2), B (-4, -4) and C (5, -8) , then the length of the median through C is
View Solution